Part II: Gathering the tools
II.1.1 We cannot achieve our objective without adopting a perspective that is fundamentally opposed to the current orthodoxy. And perhaps the best explanation for that overweening insistence that universal laws in biology are impossible comes from Bertram Murray:
… biologists tend to believe that physics is simpler than biology … allowing them to believe that universal laws and deductive theory are inappropriate in biology. But this is a misunderstanding. In fact, the physical world is extraordinarily complex. What physicists do for the physical world, which biologists do not do for theirs, is to simplify it in order to study it. …
… Newton’s mathematical model has only one planet orbiting a point in space; his physical model has only one planet revolving around one star. And Newton was correct ; the three-body problem has not yet been solved. …
…
The physical world is not simple. Physicists simplify the physical world in order to study it. Biologists do not simplify the biological world. As Dyson put the difference, “Unifiers are people whose driving passion is to find general principles which will explain everything. They are happy if they can leave the universe looking a little simpler than they found it. Diversifiers are people whose passion is to explore details. They are happy if they leave the universe a little more complicated than they found it. Biology is the natural domain of diversifiers as physics is the domain of unifiers” (Murray 2001).
II.1.2 The reason biologists cannot simplify their subject, in the way Murray suggests, is simple. They do not adequately define even the most foundational of concepts. Insufficiency of rigour then masquerades as complexity of subject.
Almost as if to make up for their predominantly nonmathematical nature, debates in biology and ecology have a long and fractious history. The parallel universes biologists occupy upon these most basic of issues is perhaps best exemplified by E.O Wilson, who adopts a very different position to Dawkins as quoted at the head of Part I:
Everyone sometimes daydreams like a scientist. Ramped up and disciplined, fantasies are the fountainhead of all creative thinking. Newton dreamed, Darwin dreamed, you dream. The images evoked are at first vague. They may shift in form and fade in and out. They grow a bit firmer when sketched as diagrams on pads of paper, and they take on life as real examples are sought and found. Pioneers in science only rarely make discoveries by extracting ideas from pure mathematics (Wilson 2013).
This unfortunate trait at biology’s heart reared its ugly head almost as soon as Darwin had announced his theory. Herbert Spencer’s ‘survival of the fittest’ might be a highly evocative phrase and a masterly abstraction, which Darwin rapidly adopted, but as others soon pointed out (Milner 1990), all it really means is that those that survive are the most likely to have survived, thus telling us nothing.
Since biology currently lacks a rigorous mathematical foundation, it is littered with uncertainties and ambiguities. Even though, for example, all “viable” biological “groups” “reproduce” and so must exhibit a “generation time”, T, not one of the concepts in quotes has a clear and/or widely accepted definition. Groups and generation time are amongst the most contentious, with different authorities volubly championing different proposals (Charlesworth 1994; Cole 1954; Dawkins 2012; Nowak, Tarnita, Wilson 2010; Pennisi 2011; Thorpe 2012). This, as Lo Bello opines, is the heart of the problem:
All mathematics begins with definitions, so that the first observation to be made about a mathematician is that he is the sort of a person who requires that all technical terms be defined, and that all common words be used properly in accordance with their accepted meanings (Lo Bello 2013).
We obviously intend to give clear definitions for the terms homomorphic, homeomorphic, and isomorphic we introduced in Part I.
II.1.3 If we are not clear about the limitations behind biology’s current perspectives and lack of clear definitions, as well as the reasons for them, then we cannot overcome them. Stephen Hawking, in his best-selling A Brief History of Time (1988), nicely characterizes biology’s somewhat parlous state of affairs:
Someone told me that each equation I included in the book would halve the sales. I therefore resolved not to have any equations at all. In the end, however, I did put in one equation, Einstein’s famous equation E = mc2. I hope that this will not scare off half my potential readers (Hawking 1988).
Granted that most biologists consider themselves clear and rigorous, this is a somewhat surprising situation. The only possible reason is a misunderstanding of what ‘rigour’ entails.
Somewhat ironically, Dawkins—who, as his above quote indicates, certainly cannot be faulted for the healthy respect he has for mathematical reasoning—provides one of the best examples of this disparity in discourse concerning the nature of rigour:
I insist on tight discipline. The criterion for recognizing a true replicator for a Darwinian model is a rigorous one. The putative replicators must vary in an openended way; the variants must exert phenotypic effects that influence their own survival; the variants must breed true and with high fidelity such that, when natural selection chooses one rather than its alternative, the impact persists through an indefinitely large number of generations (more precisely, survives at a high enough rate to keep pace with mutational degradation) (Dawkins 2004).
Dawkins’ use of ‘openended’ is immediately problematic. It beautifully summarizes matters. His “memes” illustrate the difficulty. The way he defines them is admittedly colloquially delightful, but it is scientifically unhelpful. It is—unfortunately—completely without a rigorous foundation. It strikes right at the heart of these issues. Our central concern is to remedy its manifest deficiencies.
II.1.4 There is a difference between seeing what needs to be done, and doing it with sufficient clarity and rigour. Dawkins felt it important, as a working evolutionary biologist, to pinpoint those transmissible “units of culture” that could spread through calls, traits, gestures, etc. He saw that, like genes, they could mutate, propagate, and respond to selective pressures. However, unlike genes, they were not reproductively inherited. He therefore concluded that:
We need a name for the new replicator, a noun that conveys the idea of a unit of cultural transmission, or a unit of imitation. ‘Mimeme’ comes from a suitable Greek root, but I want a monosyllable that sounds a bit like ‘gene’. I hope my classicist friends will forgive me if I abbreviate mimeme to meme (Dawkins 1989).
II.1.5 There is no questioning that biology must separate the inheritable from the noninheritable. Nevertheless, Dawkins’ ideas of “tight discipline” are rather different from what we intend. Memes do not qualify as an example of such discipline because although Dawkins has successfully highlighted the distinction between our biology and replication globes, he has given no indication of how we can use either them or his memes to make scientifically useful measurements.
II.1.6 The fault we are here highlighting—if such indeed it be—is not specific to Dawkins. It permeates an entire field of discourse that seems all too happy to leave its signally important terms inordinately vague. Hawking again gives an example:
In the eighteenth century, philosophers considered the whole of human knowledge, including science, to be their field and discussed questions such as: Did the universe have a beginning? However, in the nineteenth and twentieth centuries, science became too technical and mathematical for the philosophers, or anyone else except a few specialists. Philosophers reduced the scope of their inquiries so much that Wittgenstein, the most famous philosopher of this century, said, “The sole remaining task for philosophy is the analysis of language.” What a comedown from the great tradition of philosophy from Aristotle to Kant!” (Hawking 1988).
This is certainly a glib assessment of Wittgenstein; of the debates surrounding him; and, above all else, of the average philosopher’s ability to engage in abstractions. The essence of Wittgenstein’s argument is that while scientists and mathematicians insist upon treating planets as points because it seems to “work” very well indeed, planets are not actually points. Therefore, science is not explaining “reality”. It is either saying nothing at all, or else saying nothing of any consequence.
II.1.7 Hawking does, nevertheless, make a good point. When, for example, Henry Parker Manning produced his Geometry of Four Dimensions (Manning 1914), he was all too well aware he was leading readers into very new terrain. He therefore spoke with great clarity:
The elements of geometry are points. We do not define the term point. It is impossible to build up a system of geometry without undefined terms, and if we can give different meanings to this word we shall be able hereafter to give our geometry different interpretations. …. The objects which we study are to be regarded as consisting of points, that is, classes of points selected according to various laws from the class which includes all points. Any selected class is said to constitute a figure …. The points of a figure may also be said to lie in the figure or belong to it. One figure is said to lie in another when all of its points are points of the second. It will often be convenient to speak of a figure as consisting of certain other figures, but this expression should always be understood as meaning that it consists of the points of these other figures.
Manning tells us that points can be homomorphic. They can easily live in groups. Any figure made from points can itself be (a) a point; and (b) be composed of points. But in complete contrast to that clear usage, group remains one of the most contentious terms in all biology. It lies at the heart of the often acrimonious debate about fitness and what evolves (Dawkins 2012; Nowak, Tarnita, Wilson 2010; Pennisi 2011; Thorpe 2012). Yet the resolution seems so clear and simple. We explicitly adopted it in Figure 1: sometimes it is better to think of biological entities as composed of groups and so as homomorphic; and sometimes as clustering into groups that can then differ, from their original homomorphic ones, in their resulting homeomorphic and topological behaviours. The two together are isomorphic.
II.1.8 In face of all these difficulties, we shall adopt a simple—but we hope effective—strategy. We largely avoid using ‘group’. When we do, it will be in its strictly technical and mathematical sense.
II.1.9 We shall instead emulate Dawkins (1989) and coin neologisms, such as ‘pollency’, when we need them. We can then invest our new terms with the specific biological-mathematical meanings we desire, borrowing such rigorous terms as injective, surjective, homomorphic, homeomorphic, isomorphic and the like to tightly define them. The only test they then need to pass is the scientific one of facilitating accurate measurements, such as we do in our Brassica rapa experiments. We shall also refer to every step in building our model as one of Dawkins’ memes.
II.2.1 Since perspective is vital, then our first order of business is to describe biological behaviours in terms of our globes, our winds and wind walls, and our recurvatures, and so that we can eventually apply a set of Chomsky production rules. Our simple ambition is to give clear mathematical form to such unconscionably vague biological utterings as ‘those x entities live for time y, but produce zero descendants’. This is both vague and unsatisfactory for it gives us no way to compare entities to each other on any biologically relevant basis.
II.2.2 Meme 1, and the first step in building our model, is to define our initial nonpollent S0–V1 grouping, illustrated on Figure 1’s bottom row. We described it as both replicatively and biologically open, and as non-injective and non-surjective. Such entities are biological, but not replicative.
If our proposed nonpollent entities are indeed incapable of replicative activities, then they do not recurve to our replication globe. No matter how biologically active they might be, they can do no more than surrender to the surroundings. We must signify such behaviour appropriately … i.e. both qualitatively and quantitatively.
II.2.3 We begin by noting a contrast. Mathematical precision makes it “obvious” that 2 + 3 = 3 + 2, and that 2 - 3 ≠ 3 - 2. We therefore emulate that precision. We do so by asserting that the following Chomsky style production rule exhibits our biological but nonreplicative nonpollency:
(x × y0 → 0),
where
• ‘x’ is the number of entities;
• ‘×’ means we track them forwards or anticlockwise about the “circulation of the generations”, and so from preimage to image, but without ever entering the replication globe—i.e. by consulting their fibration, but not their cofibration—and so potentially without consulting the mapping cylinder;
• ‘y’ is their number of generations lived;
• the ‘0’ superscript means their combination of fibration and cofibration makes them intransitive—i.e. both non-injective and non-surjective—having a “reproductive index” of δ = 0;
• and the final ‘0’ means they simply dissipate from the biology globe, without themselves creating images in any progeny codomain, and so again without further use of any replication globe or mapping cylinder.
II.2.4 Since we have now defined a nonreplicative production, then Meme 2, the second step in building our model, is to assert that while the following is successfully replicative and so pollent, it is still not in balance with its surroundings. It is again not in reproductive equilibrium, for although transitive, the preimage and image and the biology and replication globes do not match. The progenitor domain and progeny codomain are clearly of different sizes meaning biological and replicative events are not bijective. They are not in a one-to-one correspondence:
(15 ÷ 43 → 40)-0.75,
where
• ‘15’ is the group of elements in the progeny codomain;
• ‘÷’ now asks us to determine their origins by tracking backwards or clockwise around the circulation from image to preimage, and so explicitly via the mapping cylinder;
• ‘4’ asks us to count back four generations or iterations across the mapping cylinder;
• ‘3’ means the group members exhibit three distinct reproductive paths;
• ‘40’ is the number of progenitors we find; and
• ‘-0.75’ means generation time shortens by 25%.
Equilibrium measurably fails because 15 ≠ 40 and ¾ ≠ 1.
We can also observe that our earlier nonpollent entities necessarily fail to attain biological equilibrium because (x × y0 → 0) can never match (0 ÷ y0 → x) since no matter what the values for x, y, or δ, we can never have 0 = x. The zero again means the replication globe recurvature, and so matching mapping cylinder activities, are never invoked.
II.2.5 The equilibrium we suggest obviously demands that we draw two such expressions—one ‘×’ and one ‘÷’—together to match two distinct journeys: one is clockwise, the other anticlockwise. One is with, and one is without, the surrounding mapping cylinder. This is a precise matching between our replication and biology globes, and our fibration and cofibration. It specifically equates homo- and homeomorphism. It is an equality between sphere and cylinder. We therefore also define it as a “doubly closed production”, for both the replication and biology globes are closed.
Meme 3 uses unipollency to define our double closure and our homo-plus-homeomorphic cylindrical–spherical equilibrium. This involves both of our recurvature journeys: one from preimage to image and back to preimage; and one from replication globe to biological one and back to replication. One journey therefore uses the intermediary mapping cylinder, while the other—at least, ostensibly—does not. This is again both homomorphic and homeomorphic and gives us our needed definition of biological and replicative closure:
π ≡ [(1 × 1δ=1 → 1)1 ⇔ (1 ÷ 1δ=1 → 1)1].
The sequence of 1s in the production on the left means:
• we consider one element in the progenitor domain;
• forwards, and so directly from preimage to image;
• for one generation, which is again forwards and could well be one anticlockwise mapping cylinder iteration, but is being explicitly considered without;
• using a bijective and singly reproductive path, δ = 1;
• ending up with one progeny or matching element in the progeny codomain; and
• with generation time holding constant.
The production on the right is then the reverse journey where we:
• begin with one element in the progeny codomain;
• track it backwards for one reverse iteration … which can now only be clockwise through the mapping cylinder, and so which is also for one iteration and generation;
• using the same singly reproductive and bijective path, with its one-to-one correspondence;
• to find a single and matching element in the progenitor domain;
• with generation time or circuit lengths again holding constant.
Since this defining population and its production has matching preimage and image and so is doubly closed, it is neither growing nor diminishing, in either numbers or time, in either direction, which is both with and without the intermediary mapping cylinder. The π means that there is—by definition—an equilibrium set of both loop and recursive interactions between the entities and their surroundings. The entities are again both homomorphic and homeomorphic. This involves no trivial cycles in either globe and so is doubly closed to them. Our biology and replication globes match.
II.2.6 Our eventual intention is, of course, to turn to the real world, and to say that since we now have a rigorously defined bijective equilibrium, π, then any real population is, by definition, also in replicative equilibrium when it similarly matches the overall events in its two globes so that:
[(x × 1δ → y)T1=1 ⇔ (y ÷ 1δ → x)T1=1] = π ≡ [(1 × 11 → 1)T2=1 ⇔ (1 ÷ 11 → 1)T2=1],
where x is the progenitors, y is the progeny, δ is some reproductive index, and the respective absolute generation lengths are T1 and T2.
II.2.7 We must now define the doubly closed entities, groups, and interactions that our model can use to produce π. This must be a group of entities with a homomorphic group structure, but that also create a transitive and homeomorphic space. Their productions can recreate both those structures and those shapes.
Since our defining entities must, and by definition, recurve in both our globes, then they must all be sufficiently like each other so they can remain near to each other at all times, both homomorphically and homeomorphically. We therefore turn to the Greek ple̅sios, meaning ‘like’, ‘near to’ or ‘neighbour’ (Busia 2014) to define them:
• “Plessists”. These are the distinct but pollent doubly closed biological entities that therefore display the homomorphic and homeomorphic metabolisms and physiologies they need to follow whatever reproductive path attains π. They are formed from countable molecules, and can engage in all relevant and observable group behaviours. They are Meme 4.
• “Plessiomes”. The molecules that can successfully both enter and reenter the replication globe to form the homomorphic and biological plessist genomes. These are Meme 5.
• “Plemes”. The meme-like traits, features, behaviours etc. that plessists enact, out in the biology globe, so they can interact both with each other and with their surroundings to homeomorphically maintain the recurvatures that produce π. They are Meme 6.
• “Plesseomes”. The homomorphic group gene pool of all the molecules in all the genomes of all the plessists maintaining π, along with a suitable distribution. Each normalized individual contribution is γ. Meme 7 then defines these plesseomes as multiple copies of γ.
• “Plessetope”. The corporate plemes representative of the plesseomes, and so creating the group homeomorphism of doubly recurvative interactions that maintains π. Each normalized individual contribution is ψ. Meme 8 defines these plessetopes as multiple copies of ψ.
• “Plessemorph”. The singular archetypal entity embodying both γ and ψ as its net set of activities λ; and so that n of them are both homomorphically and homeomorphically identical to, and representative of, all the n plessists, their plessiomes, and their plemes as maintain π, which they do by acting as nλ. The plessemorph is thus a singular and doubly closed entity. It is Meme 9.
Our plessemorphs define our doubly closed bijective biological equilibrium, π. They have homomorphic plesseomes. They interact homeomorphically both with each other and with the surroundings. They use their plessetopes to recurve, and so to recreate a matching set of preimage and progenitor domain, plus image and progeny codomain. These neither grow nor shrink, but maintain a stable state. This is a set of biological activities, λ, resulting from both ψ and γ. We can always replace a given number of plessists with a given number of plessemorphs whose behaviour across globes and domains is identical. This is so by definition in our model.
II.2.8 As a part of Memes 4 to 9, we can additionally think of our plessists and/or plessemorphs as constituting a first set, A. The material plessiomes and/or plesseomes that create them then constitute a second set, B. Their energetic and interactive plemes and/or plessetopes constitute a third set, C. We then consider the mappings: φ:A ↔ B, φ:A ↔ C, and φ:B ↔ C.
II.2.9 We can now take a first set of plessists a1 in A. We can substitute for them a set of plessemorphs aa in A that, by our model, behave identically.
Those a1 plessists have the plessiomes b1 in B … which again behave identically to our plesseomes ba in B. And our plessists use the plemes c1 in C; for which we can substitute the plessetopes ca in C.
We can then take the two sets of Cartesian products A × B × C = {(a, b, c) | a ∈ A, b ∈ B, c ∈ C} where we have the usual ordered pairs. We therefore get (a1, b1, c1) for our plessists, interacting through their plemes and plessiomes; and (aa, ba, ca) for their equivalent plessemorphs which replicate them precisely by interacting through their plesseomes and plessetopes. This is again so, by definition, in our model.
II.2.10 The a1 plessists and their equivalent aa plessemorphs can now interact with and transform each other using both the surroundings and their δ sets of Chomsky production rules of syntax and semantics to produce further sets in A, B, and C. We therefore have parallel sets of plessist and plessemorph transformations. Our plessists replicate their A, B, and C sets so that a1 → a2, b1 → b2, and c1 → c2. The plessemorphs replicate them so that aa → ab, ba → bb, and ca → cb. Their λ biological and ecological activities occur through their plessiomes and plesseomes which map through γ as b in B with all b1s mapping identically through bas; and with the plessist and plessemorph effects in the surroundings, and on each other, occurring through their pleme and plessetope behaviours mapping through ψ as c in C, the c1s again being identical to the cas. The a1 plessists thereby replicate an a2 set; with the plessemorphs equivalently replicating an ab, with all the bs once again being identical in their effects to all the 2s that repalce the 1s. Those interact with the surroundings as a2 and ab in A, using b2 and bb in B, and c2 and cb in C, through the same biology-ecology of λ, mapping as γ in B and ψ in C. These also contribute to the fibration, θ and cofibration, ρ so that we will eventually have replicated replacements of a3 and ac in A, b3 and bc in B, and c3 and cc in C, again preserving equivalences in mappings of γ, ψ, λ, θ and ρ through the same Cartesian products over the same three sets A, B, and C. The latter can substitute for the former at every point.
II.2.11 This is all clear, precise, and tightly defined. All we have to do now is relate one or the other of our plessists and/or plessemorphs a1 and aa to some real and existent biological phenomena. For that, we can turn to topology.
II.3.1 We now have our plessists and plessemorphs and their various A, B, and C sets and production rules. They recurve in our two globes, using their biological–ecological relations λ, made up from their energetic plemes and plessetops ψ, and their material plessiomes and plesseomes, γ. The latter can again substitute for the former in every conceivable situation.
II.3.2 Nothing underscores the need for the careful approach we adopt here than the circumstances surrounding René Thom (Johnson 2002). Winner of a Fields medal, his principal mathematical fields were “cobordism” and “catastrophe theory”. He coined the word ‘attractor’, and was the most famous and influential of those who introduced biologists to topology (Thom 1969). His work proved influential not just in morphology, but also in the study of punctuated equilibria. His Structural Stability and Morphogenesis (1989) pointed out that even though natural phenomena are always subject to perturbations, they can nevertheless be represented by gradually changing forces. So in spite of all developmental changes, morphological phenomena preserve a basic identity. What was exciting to biologists was that small but continuous changes in parameters could produce significant qualitative ones. Such was the power of Thom’s mathematically accurate formulations that there was no need to know the underlying physical mechanism for even the most abrupt and discontinuous of transformations. A simple mathematical description subsumed even the most complex of physical processes.
II.3.3 Biologists and mathematicians both classify objects into groups. But while Thom might have brought with him a very strict and mathematically coherent understanding of how mathematicians used the term, he was now working amongst people whose standard for providing definitions was considerably more relaxed—to say the least—than his own. By his own admission, however, that was precisely the reason he left pure mathematics:
… I had nothing new to offer. That made me leave the strictly mathematical world and tackle more general notions, like the theory of morphogenesis, a subject which interested me more and led me towards a very general form of ‘philosophical’ biology (Thom 1958).
Some biologists, such as Francis Crick, dismissed Thom for criticizing the lax usage he came across. They instead criticized him in return for “not really understanding” how science worked (Johnson 2002). But they in their turn never saw the importance of emulating the utmost care that mathematicians and physicists take in, for example, defining velocity and acceleration … never mind homomorphism and homeomorphism. It is, however, precisely those careful definitions that make the rudiments of both dynamics and topology appear so “simple” that the rigour they insist on is trivialized by deeming biology so complex, a similar search for clarity is inappropriate.
II.3.4 Much like species, different mathematical groups behave in different ways. Thom’s understanding came directly from the tradition of the French mathematician Évariste Galois who was the first to use the term group in relation to equations such as:
x2 - 4x + 1.
Galois pointed out that all constants form a first group; coefficients a second; variables a third; and powers a fourth. The different groups thus exhibit different production rules.
“Group theory” now refers, more broadly, to the theory of symmetry. This means virtually any activity subject to any kind of repetition. For that reason, its logic undergirds all scientific inquiry. All scientific laws are governed by group theory.
Group theory is the search for—and mathematical formulation of—internal consistency. It declares an invariance in objects. We are now searching for the internal consistency that drives our plessists and plessemorphs.
Group theory tells us, on this basis, that the above equation’s two solutions form the two groups A = 2 + √3 and B = 2 - √3. Bringing them together into a single group establishes a pattern of invariance. Their group behaviour is that even though 2 - √3 ≠ -√3 - 2 and 2 ÷ √3 ≠ √3 ÷ 2, all similar algebraic equations with rational coefficients will always have A + B = B + A, and AB = BA. This “Galois group” forms cyclic permutations of order two. We note carefully those forwards and backwards operations, which are effectively recurvatures. They have the same result, no matter what the direction.
II.3.5 Both the above groups A and B enjoy a joint identity that leaves them untouched when transposed. And that statement about identity is critical. It is a concept utterly lacking in biological groups. What, after all, do biologists imply when they assert that a given group is “female”, never mind that another forms a “species”? Some organisms alternate sexes in generations; others invert male-female sizes and capabilities; yet others do not have either male or female reproductive parts; yet others still develop them according to circumstance; and so on and so forth for a bewildering variety. And without a clear identity even for specifying female, what hope for species?
II.3.6 Biology’s failure to formalize an identity is most surprising, for one already exists. It was early recognized by Robert Hooke, who dramatically developed the microscope and observed microscopic organisms. His Micrographia (1665) was the first comprehensive and illustrated book in microscopy. But not being a mathematician, he did not realize his discovery’s formal significance, although he did calculate that there must be 1,259,712,000 in a cubic inch (Inwood 2003).
The fuller recognition of the biological significance of cells—via his famous aphorism omnis cellula e cellula or “every cell stems from another cell”—did actually come from the pen and mind of Rudolf Virchow (1859). But granted that it was Hooke who first coined the word, then our Meme 10 is to term biology’s unipollent-based doubly closed identity—which defines our plessemorphs, and their plesseomes and plessetopes—the “Hooke cell”. The Hooke cell, therefore, is our rigorously defined unipollent equilibrium and biological archetype. Since it is dynamic it by definition encompasses recurvatures in λ, ψ, and γ.
II.3.7 To see that a Hooke cell is indeed an identity—for it is both homomorphic and homeomorphic—then we first note that 1 + 0 = 1. Zero is an “identity element”. We further observe that we can introduce infinitely many zeros, and it will make no difference to the original: 1 + 0∞ times = 1. An identity therefore leaves things unchanged. The clear implication is that we can similarly take species, S, as some sort of identity, S’, for our plessemorphs, plesseomes, and plessetopes as produce it. We can reproduce them infinitely many times, and the species remains the same.
II.3.8 Identities—as do species—allow for replication. Thus zero, as an “additive identity”, also allows us to replicate its operative groups. We see this clearly in 3 + 0 + 0 + 0 = 3 and 2 + 0 + 0 = 2. If we now count up all the inserted identity elements, they will reproduce the implied 2 + 3 = 5 as 5 + 05 times = 5. The inserted identities have replicated the originals, leaving them unchanged. This holds for any x and y. An identity immediately allows the production rule and mapping φ:X → X leaving everything the same. Much more importantly, identities allow for symmetry operations for they leave aspects invariant through transformations.
This operation of addition and its additive identity allows us to note that if we for example take n = 6 and consider the “binary operation” of addition modulo 6, we form the cyclic group Z6 = {0, 1, 2, 3, 4, 5}. This simply means that if we consider that first element of ‘0’, then the numbers ‘6’, ‘12’, ‘18’, …, all leave zero remainder when divided by 6. And since all numbers divisible by 6 behave this same way, we can group them together as a “cyclic subgroup”.
If we now add any members of this cyclic subgroup to each other, we get 0, because 6 + 12 = 18, all three of which are divisible by 6. Since this is the same for all such numbers, then the group generated by this operation by element 0 in Z6 is <0> = {0}. In other words, we can do this infinitely many times—24 + 36 + (n × 120)—and only ever generate—or replicate—the group identity.
The number 11, on the other hand, leaves a remainder of 5 when divided by 6, which is the last member of the Z6 cyclic group. The numbers 17, 23 etc. all leave that same remainder. They can all therefore be classed as members of the same cyclic subgroup.
If we now add any member of this latest cyclic subgroup to any other member, we get the equivalent of 5 + 5 = 10, which leaves a remainder of 4. And if we now add that remainder to any member of this same subgroup, we get 4 + 5 = 9, which has a remainder of 3. And if we then add whatever remainder we get successively to each member of this same subgroup, then we get 2; then 1; and we eventually finish up with a number divisible by 6. So using 5 as a generator, we step through—or replicate—all elements in this Z6 cyclic group to give <5> = {5, 4, 3, 2, 1, 0}.
The numbers 4, 3, and 2 in Z6 are very different. When we for example add 4 to any other element in its same cyclic subgroup, we get 4 + 4 = 8, which is a number whose remainder is 2, modulo 6. And if we add that remainder, yet again, to any member of this same subgroup, we get a number divisible by 6, which is zero, so giving <4> = {4, 2, 0}. We have this time only generated a limited selection in Z6. We see the same limited generation capacity in <3> = {3, 0} and <2> = {2, 4, 0}.
We can, however, once again generate the entirety of Z6 if we consider 7, 13, 19, etc, which all leave a remainder of 1 modulo 6. If we add any two of these subgroup members together, we get something like 13 + 19 = 32, which is modulo 6 equivalent to 1 + 1 = 2. And if we now add that 2 remainder to any other member in this same cyclic subgroup, we get something with a remainder of 3; then 4; then 5. So we again generate the entire set, to give <1> = {1, 2, 3, 4, 5, 0}.
There will always be two members in any such cyclic group that will form cyclic subgroups such that they generate the entire group. We shall soon see that all biological entities form infinite, rather than finite, cyclic groups and subgroups of exactly this kind.
II.3.9 A similar identity and replication pattern gives us 1 × 1 = 1, with unity now being the “multiplicative identity”. We can again insert it infinitely many times, making no difference to the original, as in 1 × 1∞ times = 1. And if we insert it an appropriate number of times it becomes a replicator for we can turn both 3 × 1 = 3 and 2 × 1 = 2 into 3 × 1 × 1 × 1 = 3 and 2 × 1 × 1 = 2. We have successfully reproduced the implied 6 × 16 times = 6 … while leaving the original utterly untouched. This holds, as above, for any x and y. We get similar cyclic groups, subgroups, and generators. We have confirmed an important identity–replication production rule.
II.3.10 Integration and differentiation are admittedly slightly more complex, but the same principles apply. Leonhard Euler realized the full consequences of e being the exponential identity element for such operations. We can express any initial function f1 (x) and its differential dx as some second function, f2(x), that is then a power of e. For example, 1⁄x = 1⁄elognx = 1⁄ef2(×) = 1⁄f1’(f2(x)) = f2’(x). We can replicate this infinitely many times, as ever leaving the original unchanged. There are similar cyclic groups and subgroups. So as we can with the above identities and cyclic groups, we can always generate the original and therefore replicate it any number of times, both always leaving the original unchanged and generating the entire group.
Euler’s discovery is extremely useful biologically. It helps guarantee both homo- and homeomorphisms. We can express any growth or development continuously and exponentially as a range between 0 and 1, or between “unit limits”. We can therefore evaluate any organism by recasting its behaviours as a “unit expression”, and/or inserting that unit expression appropriately many times into a suitable equation, while, as ever, leaving the original unchanged.
We are well on the way to relicating any biological phenomenon by expressing its rate of change between 0 and 1. It then matches the unipollent. We can compare the two and determine pollencies in terms of injective and surjective behaviours. We can also repeat it an arbitrary number of times, and it remains unchanged. We can therefore use it to carefully define our needed four-dimensional biological equilibrium, as well as find and define our infinite cyclic groups and subgroups.
II.3.11 A big problem would seem to be that even if we can separate the biological from the replicative, the globes can vary very greatly across the generations. But it is also thanks to Euler that a topological identity and invariant to resolve this came to exist. It is now known as the “deformation retract”. As in Figures 1, 4 and 5, it allows us to manipulate any object—in our case between and/or within our replication and/or biology globes—without losing any of its essential characteristics. The points simply create infinite cyclic groups and subgroups.
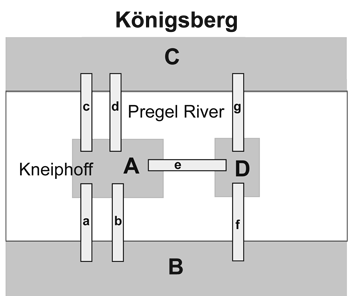
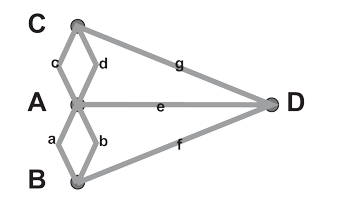
II.3.12 Topology began in earnest in 1735 when the mathematician and astronomer Carl Gottlieb Ehler presented Euler with the then unsolved problem of the “Seven Bridges of Knigsberg” shown in Figure 4. Euler famously solved it using a variant of the network or stylized map in Figure 5. He had realized that each landmass is homeomorphic. Since the number of points in each is irrelevant, each can be—homomorphically—regarded as a single point … but each can, for that same reason, be replicated an arbitrary number of times, leaving the original unchanged. This means each can be regarded both as a single point, and an arbitrary collection of such points, irrespective of sizes or shapes.
Topology discusses the relationships between groups and sets of points. Euler proved that when all similar groups of objects—both homomorphic and homeomorphic—are expressed as sets, then they have an “Euler characteristic”. In this Knigsberg case the sets are landmasses that form sets of homomorphic vertices, |V|; the bridges form homeomorphic edges, |E|; and the areas between them form homeomorphic faces |F|. The relevant production rule for an Euler characteristic is:
χ = |V| - |E| + |F|.
The Knigsberg bridge case gives χ = 4 - 7 + 4 = 1.
Euler had thus elucidated the four important topological principles that:
I. the number of vertices is critical;
II. each bridge’s length is irrelevant;
III. landmass sizes and shapes are irrelevant;
IV. each landmass can be reduced to a single vertex.
Topology’s deformation retract is implied by III and IV. If two objects are topologically identical then they will have the same Euler characteristic. This means the same production or replication rule.
Since “fixity of shapes” (note similarity to “fixity of species”) is irrelevant in topology, then we can both homomorphically and homeomorphically replicate any object, leaving the original unchanged. We can add—and remove—infinitely many points to, and from, the edges, and/or the faces, of any figure or network without affecting any of its essential properties.
II.3.13 Since we are particularly concerned with biological reproduction—which particularly involves cyclic groups and subgroups—then we most carefully note that we cannot proceed randomly. Simply having the same Euler characteristic does not automatically mean two objects, as sets of points, are topologically identical. A tetrahedon, a cube or hexahedron, an octahedron, and a dodecahedron are very different, but they all have χ = 2. Not all globes and generations, therefore, need be the same.
If we have an original set of points X; and a subset Y; if we use an index, i, to range a map, Mλ, between them; and if every element x in X maps to some y in Y as we range that index between i0 and i1; then we can only preserve homeomorphism, amongst those points, if subset Y is the deformation retract of X. However, since two groups of points can have the same Euler characteristic χ without being topologically equivalent, then as in the Knigsberg Bridge problem, we must specify that our mapping, Mλ, is the continuous Mλ:X × [0, 1] → X, with Mλ(x, i) = mi(x) = 0 to mi(y) = y for all y in Y, and from i0 (X) = 0 right through to i1(X) = Y. The two will now have the same Euler characteristic, such that χ(X) = χ(Y).
But we additionally preserve homeomorphism in the above case because the i0 is mapping i0(X) directly onto i0(Y). That is the identity map that guarantees they are homeomorphic.
The deformation retract is the special, contained, identity map equivalence. It helps guarantee that both our syntax and our semantics have stayed the same in the resulting production rule, and no matter what transformations our biology and replication globes might go through.
II.3.14 If we represent our group operation, much more generally, by ◦, then we can say, equally generally, that any set or group, X, has the identity property, under that particular operation, ◦, if an element, #, exists that leaves every other element x in X unchanged, and such that both x ◦ # = x and # ◦ x = x, again for all elements x in X.
As we did with 1 + 0∞ times = 1 and 1 × 1∞ times = 1, we can now use # as an index into all the x in X, as x ◦ #x times = x. We can now replicate any X as a Y. There will then be a y in Y for every x in X, with # guaranteeing that identity.
An identity’s ability to replicate any group is the aspect of especial relevance here. It is how we can use a Hooke cell to guarantee the reproduction of identical objects.
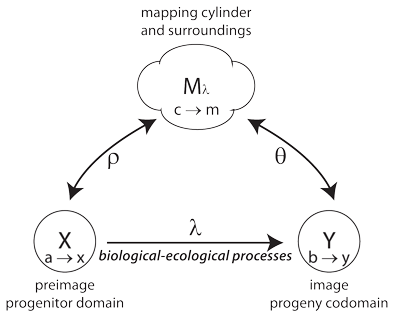
II.3.15 As in Figure 6, the deformation retract and mapping cylinder work together. If X, as a preimage, maps to Y, as an image, using the proposed biological-ecological process λ, then a mapping cylinder Mλ exists to describe that process. We can also conceive of it as the interaction with those same surroundings.
If Y now has a set of combined internal and external operations, θ, that allow it to access neighbourhoods in its mapping cylinder, Mλ, then X can in its turn use its identity, #, to map to those self-same neighbourhoods in that same mapping cylinder. In other words, X can use the surroundings, Mλ, to replicate Y … which then appears as if a set of biological-ecological operations, λ, have seemingly carried X directly into Y, as the group operation, ◦. One of those operations is with the mapping cylinder, the other is without. One is a direct and intrinsic transformation, the other an indirect and extrinsic one.
The operation that “lifts” from Y, as the image, to the mapping cylinder is its fibration, θ. It means that there exists a continuous function between Y and Mλ—or the surroundings—so that given a point y in Y and a unit path [0,1] that started at some point b in Y to reach y, then that path can be lifted to one starting at some c in Mλ, and that goes faultlessly to m in Mλ, over that same 0 to 1 range.
The ρ that similarly lifts from the preimage X to that same mapping cylinder Mλ, over the same range and in the same fashion, and so from a to x in X to give the same c to m in Mλ, is its “cofibration”. Each of a, b, and c, and x, y, and m, respectively, are equivalent over all those equally equivalent unit expressions.
And if X now uses λ to directly map to Y; and if Y is indeed a deformation retract—which we can express equivalently as # or S’—for the mapping cylinder, Mλ; then a cofibration, ρ, again exists such that Mλ can accept a mapping from X; and with Y then mapping, with its fibration, θ, to those same points in Mλ. The surroundings are again permitting that transformation.
And alternatively … if a cofibration ρ exists that can ostensibly replace the biology-ecology of λ … then a mapping cylinder, Mλ, must also exist that regards Y as its deformation retract, complete with a θ fibration. The mapping from X to Y through Mλ, using ρ, can now substitute for λ in all possible situations; and with Y also being able to map to Mλ through θ. We have now suitably redefined all aa, ba, and ca plessemorph, plesseome, and plessetope behaviours in A, B, and C both (a) directly between X and Y as a set of replicative operations; and (b) indirectly through the biology and ecology of the surroundings, as Mλ. They can therefore, and at any time, substitute for our a1, b1, and c1 plessists, plessiomes and plemes; and conversely.
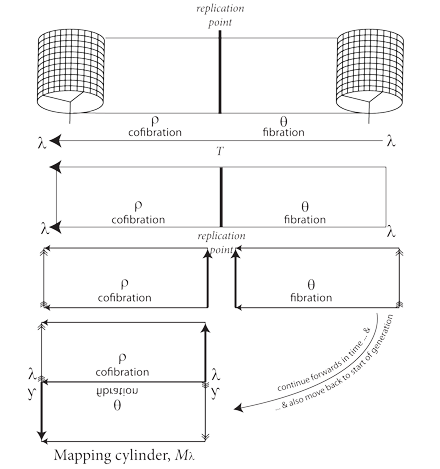
II.3.16 We somehow have to separate the purely biological transformations from the ones that, while also biological, are additionally replicative. Figure 7 shows how we can do this using such a mapping cylinder. We simply separate the temporal issues of traversing a generation from the more structural biological-replicative and transformational ones. We can do this in four dimensions because they are simply different directions.
II.3.17 We first consider the more familiar three-dimensional case. Since any sphere contacts any lower and two-dimensioned planar surface in a single point, then a cylinder of specified volume and radius can substitute for that same sphere at that contact point. The two are indistinguishable, again at that point. This holds all about any circulation or orbit. This holds throughout our three-dimensional “realm”, with its three x, y, and z dimensions.
As in Figure 7, when an ordinary three-dimensional chariot wheel or cylinder, as substitute for some globe’s contact point, rolls along a two-dimensional surface, we get a rectangular trail. We have both a beginning and an end to the generation.
We then take up that resulting rectangle. The replication point sits in the middle. This simply means that the first part, our fibration, leads up to that point; while the second half, our cofibration, leads away. The two match in that since our overall biological-ecological operations are λ, we now have λ = θ + ρ, with the replication point acting as their combination. It effects their transition. They together carry the population through the biology and replication globes for a generation.
We now create our Mλ mapping cylinder by cutting that rectangle in two at that replication point. Neither θ nor ρ lose their ability to generate λ. No more so do the biology and replication globes. They can both still—together—generate the whole of λ.
We then reattach the half-rectangle we get as shown. Since neither of the biology and replication globes has lost its individual abilities, they simply create a different interfacing combination. Each of their activity sets still leads to and away from their new junction. We are simply focusing on different aspects of these same phenomena. We can still move forwards in time, and so to the beginning of a new generation. We can still move in that direction along the arrow in the middle.
We also now have a Möbius strip. We can use it, with its rearranged infinite cyclic subgroups, for our recursive functions. They still allocate both the fibrations and cofibrations, and the biology and replication globes, to the same λ through the interfaces to have the same effects in the surroundings. They still generate the original infinite cyclic group. We can again easily get the original generation back. Furthermore, these are our plessists and plessemorphs that we created with our identity operations, leaving the originals untouched, so that nothing in the real world has changed.
II.3.18 We can now step up a dimension. We can at any time consider our four-dimensional and biological hyperglobe to instead be a “cubinder” or “hypercylinder”—the four-dimensional equivalent of a chariot wheel or tire—that contacts our three-dimensional “realm” at our precise location. A cubinder is simply a four-dimensional cylinder. As it rolls through our three-dimensional realm, it leaves behind it not a rectangle, but a cube.
We can use the resulting cube to create a mapping cylinder, for our interactions. We cut the resulting cube in two; twist it about; and then reattach it. We reorganize our various cyclic subgroups. We also create a Klein bottle.
II.3.19 We can now think of the biology and ecology of our identity–plus–deformation retract to mapping cylinder–plus–surroundings interaction as an expression of this cyclic subgroup rearrangement. We have a bounding but four-dimensional biology-replication transformational globe interface. It stretches across that mapping cylinder. It identically replicates the more familiar temporal–generational one when it contacts our three-dimensional realm.
If we now use the identity, or deformation retract, as a mediator for all λ interactions in the surroundings, then we can regard any two successions of biological elements as one of preimage to image, and image back to preimage. A generation is a set of productions that deform, directly and successively, into each other across the Möbius strip or Klein bottle through ρ. Those elements still use the surroundings as a mapping cylinder. They still map directly from X to Y. They have successively accessed each other through θ and ρ, still guided by the same mapping cylinder as before, and by the same deformation retract. They have still processed in the same surroundings, over the same stretch of absolute clock time, for the same complete generation, and using the same set of biological-ecological activities, λ.
Our progenitor to progeny or X to Y four-dimensional and recursive function production still appears as the same set of correctly constituted forwards-directed three-dimensional λ loops emerging through our cylinder and biosurfaces, S. The loops they provide still appear as if they have been produced directly by—and as—the entities concerned. Those production rules can recurve as all the needed progeny–to–progenitor and reversing transitions, and as if through the fibrations and cofibrations θ and ρ, so creating all identical events in biology and ecology. We can now examine both sets of interfaces—the familiar temporal one and the unfamiliar atemporal one—much more closely.
II.4.1 Now we know the rules and have some clear terms, we can easily define biological reproduction as a suitable recurvature. Our plessists will then respect both homomorphism and homeomorphism, as well as that change of boundaries that creates our mapping cylinders and deformation retracts. We can also soon redefine reproduction as both (i) our cofibration, ρ, plus mapping cylinder,Mλ; and (ii) our Hooke cell, or deformation retract, S’, plus its fibration, θ.
II.4.2 As our first step in defining our mapping cylinder and its Möbius strip, we formally recognize, for Meme 11, our Hooke cell’s ability to pass first into, and then through, both of our replication and biology globes, and so our infinite cyclic groups and subgroups.
We can rigorously define this capability by noting that the plessists that create our doubly closed π equilibrium must undertake a suite of reversible fibration–cofibration metabolic and physiological processes. More specifically, this must be a set of activities that always appears to bound a region of activity and so potentially seems to create a trivial cycle, but that can nevertheless have a velocity and an acceleration that carries it all about both globes.
We can attain our ambitions if we characterize one set of activities as internal and so semantic. These are our biovolumes, V. We can then characterize the other as external and syntactic. Those impinge upon the surroundings through our biosurfaces, S. These are then our needed recurvature and invertible interactions involving the boundary between our biology and replication globes.
II.4.3 We can use the homeomorphism, and the surroundings, to define our homomorphism, and so our deformation retract. We represent one globe and its infinite cyclic subgroups with x; another with y. We simply say that when our plessists surrender any initial atom or joule, x-1 or y-1, through their surface, S, they immediately take up another of exactly the same type, through that same surface, as x1 or y1. Since homomorphism demands that the structure remain identical, then these recurvature replacements x1 and/or y1 precisely replace the x-1 and/or y-1 ones that departed, passing through the surface, and where x-1 ≡ x1 and y-1 ≡ y1. Our cyclic subgroups thus regenerate the identical infinite cyclic group and volume, V, which then has the identical relationship to its subgroups and surface.
We now call the input point that achieves our recurvature replacement +r, its output -r. And since they must both be both homomorphic and homeomorphic, then they are together both (a) the homomorphic point S0; and (b) the homeomorphic “pointspace” V0. At the end of some given period, T, our Hooke cell has enacted our unipollent S0–V0 process with its (x-1, y-1) → (x1, y1) production rule to replicate itself.
This exchange of x and y, through +r and -r—whether as single and direct homomorphic point S0, or the recurvature capable homeomorphic pointspace V0—is our identity process, #. Each Hooke cell leaves both itself and its surroundings utterly unchanged, for we by definition have both x ◦ # = # ◦ x = x, and y ◦ # = # ◦ y = y. And since this is a clearly defined identity operation involving our mapping cylinder, Mλ, then the end result is in all respects identical … save only for being composed of a completely different set of both joules and chemical components. Our Hooke cell has been both homomorphically and homoeomorphically recurved and transformed using fibration, cofibration, and a mapping cylinder. The Hooke cell—which by definition incorporates both (a) some time period, T, and (b) an entire suite and cycle of activities—is therefore our deformation retract. The surroundings are also and by definition its mapping cylinder, Mλ.
We can express this in a more useful fashion. We note that our Hooke cell undertakes both a fibration and a cofibration as it goes through its recurvature involving both x and y. Since the Hooke cell is an identity, involving the biology and replication globes, then it also allows us to reconstruct any arbitrary biological entity as a plessist … whilst all the time leaving the original unchanged. Since a cyclic subgroup can generate every element in its group, then for every molecule and photon we extract we insert an identical one; and for every one we insert, we extract an identical. We can therefore generate the original, leaving it unchanged. And since, for every x, there is both a +y and a -y; while, for every y, there is both a +x and a -x; then we are more technically demanding that this Hooke cell be an irreducible and real analytic set, which is never singly pure-dimensioned.
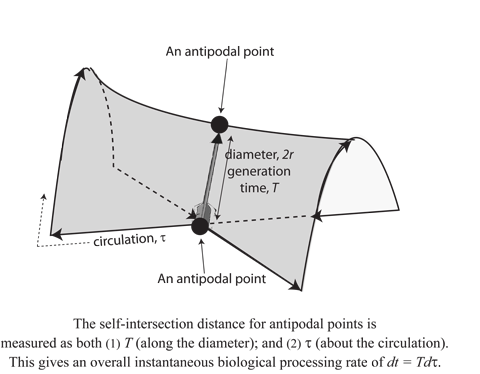
II.4.4 Figure 8 shows a “Whitney umbrella” (Weisstein 2015c) with exactly these properties. Named for its discoverer, the US mathematician Hassler Whitney, it is a ruled surface for it can be generated by a straight line moving up and down. It has an Euler characteristic χ = -1 and establishes a “pinch point” (Weisstein 2015b). It can open out to reveal its +r and -r properties, as the pointspace, V0; while still also collapsing to become a single pinch point, S0. This is therefore an S0–V0 coupling. As required, it leaves everything identical.
Meme 12 is now to recognize that the same Whitney umbrella and its S0–V0 pinch point can be in different states. It can be distinct -r and +r “antipodal points” as its contrasting but homomorphic attributes go through their homeomorphic cycles. But since each antipodal pinch point V0 pairing can retract to a single S0 one, then all such +r and -r opposites are in some respects the same. Each antipodal point plus the 2r distance between them forms a triplet that is simultaneously a singlet. It can exchange both x and y with the surroundings, but act as a single +r–-r unit.
Figure 8’s recurvature creates a rectangle of specified size. And when observed in three dimensions, that rectangle passes through itself. Since it is created by a straight line both moving up and down and circulating about, then it is composed of two different sets of “field principles”:
• one radial, ψ, which establishes the diameter, T, and can provide a velocity;
• and one circulating, γ, which establishes the bound so that can recurve.
The rectangle when acting as a pinch point can either go directly from preimage to image or vice versa as λ over T; or it can circulate about by using its fibration and cofibration, θ and ρ.
II.4.5 The first field principle in our Whitney umbrella, ψ, is structural. It is homomorphic. It is radial and radiative, directly linking the two discernible +r and -r points. They have opposite but attracting properties. They together create the central pinch point over T. One is a net donor, and so positive; the other a net recipient, and so negative, with the one therefore attracting the other.
Since this first radiative principle involves an interaction with the surroundings, then it has a syntactic biological and surface effect in time. We therefore define it via the measurable force it exerts with its two opposites. This is via whatever material objects we find at the destination. Their direction of action is set by the direction of the force that a first object exerts upon any second. The quantity is determined from those effects that the first has upon the second. This can now easily be from a progenitor domain to progeny codomain, or vice versa. In an equilibrium case, the various cyclic subgroups form the total of zero as well as the cyclic group itself: +r - r = 0.
II.4.6 Our Whitney umbrella’s second field principle, γ, is spatial. It is circulating and so produces the wind walls and recurves. It is homeomorphic. It is more concerned with defining a suite. But it again links opposite and attracting points, interacting with the surroundings. It is similarly defined via the measurable and cyclical force it exerts in the surroundings.
This second spatial and homeomorphic force differs importantly from the first structural and homomorphic one for it binds and couples through spaces to produce that same pinch point. Since only its couplings exist, it produces circular looping fields. It can therefore oversee all progenitor–progeny transformations. The equilibrium case has ∫dS = 0.
Our Whitney umbrella and pinch points create—and are—our plessists. Since our cyclic subgroups produce the cyclic group as +r - r = ∫dS = 0, then they together form a variety of lines, surfaces, and volumes as they interact both with each other and with the surroundings.
We can put this another way. Every point in a Whitney umbrella is located relative to specified others close to it in its neighbourhood … but each simultaneously displays its antipodal values relative to given others and their antipodal neighbourhoods. These points and their antipodes are also mutually substitutable for each other in given contexts. Meme 13 is therefore to call this identity pinch point and group operation, ◦ or λ, a “self-intersection”.
Meme 14 is now to recognize that all self-intersections must also have a joint identity element, #. All the various infinite cyclic subgroups can always come together to produce zero. But that also means each point can be in at least two different, but equivalent, states to create such a neighbourhood and identity.
II.4.7 These inevitabilities now permit us to resolve problems of the general kind shown in Figure 9, which is simply a different representation of the same recurvature and pinch point. It is the same irreducible real analytic non-singly dimensioned Whitney umbrella of Figure 8. The circuits about each are the same. The V0 pointspace based +r-r self-intersection journey about Figure 8’s boundary is exactly an S0 journey up Figure 9’s helicoid. The net sum on that axis is still zero, as also the sum of the surrounding recurvatures.
If we catch hold of either of Figure 9’s arrow’s tip or tail—of value S’—and push or pull, then we create or remove helicoid levels … which are also transfers both directly and as recurvatures between preimage and image; or conversely. Each vertical point on a helicoid is identical to the ones directly above and beneath it, whilst being antipodal to all those diametrically across. The two operations are in all respects identical, with S’ ≡ #, and +r - r = ∫dS = 0.
Our group members now share both (a) the same average magnitudes, S’, and (b) the same average differentials dS’ about their pinch points. Since they are both homomorphic and homeomorphic, they use their self-intersections to recreate neighbours, neighbourhoods, antipodal points, and helicoid levels using fibrations, cofibrations, mapping cylinders, and deformation retracts.
Our mapping cylinder is all of the helicoid sitting about the deformation retract, which is again both (a) the central axis, and (b) the white middle track. That spiral helix forms the right helicoid that sums as ∫dS = 0. Those values at its centre create the +r - r = S’ which is the median value about which they oscillate. It is again the axial values.
Memes 15 and 16 recognize that the helicoid and self-intersection diameters, T, and the circulation distances and helicoid orbits, τ, which jointly construct those preimage and image exchanges are not fixed. Dawkins’ unacceptably vague “openended” has become the topologically precise homeomorphic declaration that these are always antipodal neighbourhoods linking τ and T.
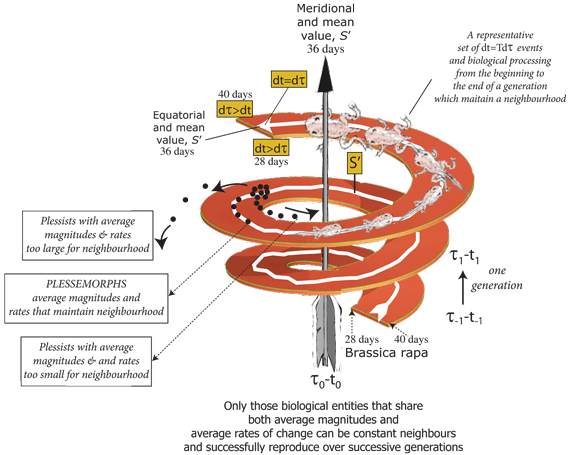
II.4.8 We can frame a first hypothesis to explain why Brassica rapa’s generation length varies between 28 and 40 days: plessists with larger initial magnitudes, which are therefore on the helicoid outside track, must also have smaller rates of change—meaning a longer series of smaller dτ increments—across that longer T. They take longer to self-intersect. Plessists with smaller initial magnitudes, which are therefore on the inside helicoid track, have correspondingly larger rates of change across a shorter T—meaning a shorter series of larger dτ increments—and so self-intersect the more rapidly. These differences are therefore “variations”.
We can also hypothesize that those behaviours tending to the outer track, which is one set of antipodal points and values, delay self-intersections and so are characteristically female; while those tending to the inner track or opposite set of antipodal points instead advance self-intersection, and so are characteristically male. As members of infinite cyclic subgroups, they together give +r - r = ∫dS = 0. This can be subjected to rigorous testing.
II.5.1 The true difficulty for our model—as in all biology—lies in placing biological entities into suitable groups—both qualitative and quantitative—that can generate suitably replicative and recurvature behaviours. So our next step, Meme 17—in creating our Möbius strip and the inversion we see in the Whitney umbrella—is to recognize reproduction as the joint fibration–cofibration, and boundary interactions. We also recognize that, irrespective of any apparent differences, it is also the joint interaction between Subpopulations M and N upon Figure 9’s inner and outer helicoid tracks. They have an average self-intersection time, T’. It is the species average state and identity, S’ which constructs the right helicoid. It is (a) the distance up the self-intersection’s midline, and (b) its bounding length; and also (c) the time up the helicoid’s meridian, and (d) the central value about the helicoid track. In Brassica rapa’s case, these are all T’ = 36 days.
The Möbius strip also arises because entities with lesser initial magnitudes, starting their recurvatures on the helicoid inside track, must compensate with higher rates of change so they can tend towards those with greater initial magnitudes, and that therefore have different recurvature rates. In the same way, those with the greater initial magnitudes, starting their recurvatures on the outside track, must have lower rates of change so they can tend towards those beginning with lesser initial magnitudes. The equatorial T’ = 36 days track is, by definition, the equilibrium self-intersecting and recurvature path a Hooke cell would pursue under similar conditions. It is the value we use to add or remove antipodal points and equilibrium helicoid levels.
II.5.2 Since the recurvature distance, τ, about either a self-intersection or a helicoid track is a set of fibration–cofibration activities that go all about a closed path, then it is a “linespace”. It is technically also called a “circulation”. The entire linespace is therefore our circulation of the generations.
The plessists in the progenitor domain will transform from their initial preimage state S-1 to become those in the progeny codomain with the final image state S1. Every absolute time interval, dt, involved will contain a given amount of fibration–cofibration biological processing, dτ. The precise amount will depend on the generation length, T, and will be dt = Tdτ.
Any two Subpopulations M and N will have the set of individual plessiomes, plemes, and rates S’M, S’N, dS’M⁄dτM, dS’N⁄dτN, dS’M⁄dtM, and dS’N⁄dtN. Since entities with smaller magnitudes must self-intersect with, and recurve about, those with larger magnitudes, the entities within the subpopulations must maintain rates across the circulation distances τM and τN, and the historical epochs TM and TN respectively. The two rates dtM = TMdτM and dtN = TNdτN link the population circulation distance τMN and absolute time TMN via dtMN = TMNdτMN.
The necessary self-intersection and recurvature distances again require the Whitney umbrella and Möbius strip. Our two subpopulations M and N will have archetypal plessemorphs, plesseomes, and plessetopes that define the right helicoid track, and the Whitney umbrella boundary. These attain their equilibrium state. They share the same production rule. This is the joint magnitudes and rates S’MN, dS’MN⁄dτMN and dS’MN⁄dtMN. All these form a group. Their group operation of ◦ could also be the Chomsky production rule, δ.
II.6.1 The power of group theory is that it is a search not for any particular laws, but simply for a commonality. The symmetries it seeks are not always trivially evident. But they are both universal and nonmetric. They emphasize relationships based on a well-defined invariance.
II.6.2 Even those biologists who advocate the most strongly for gene supremacy agree that biological groupings are important on at least some level. And similarly, those who advocate for group supremacy agree that even the most widespread of their much beloved sociobiological behaviours can be validly described at both the gene and the individual levels.
II.6.3 Since our plessists will not be useful unless they can address these group issues, then our Memes 18 and 19 stipulate that our plessists—which form rigorously defined infinite cyclic groups and subgroups—interact with the surrounding world to create their mapping cylinder, Mλ, and deformation retract, S’. The two memes also decree that plessists abide by the scientific doctrine endorsed by the Nobel Prize Committee that:
The behaviour of the individual constituents that make up our world—atoms (matter) and photons (light)—is described by quantum mechanics. These particles are rarely isolated and usually interact strongly with their environment” (Class for Physics 2012).
Meme 18 now calls photons ‘Ingredient 3’; while Meme 19 calls atoms ‘Ingredient 4’. We further define Ingredient 3 as the radiative, ψ, component in our Whitney umbrella. It can now easily supervise the replacements of all Ingredients 4. We then define those Ingredients 4 as the circulating γ component. The two together can now propagate as λ … again in the Whitney umbrella, and as its overall presentation. The former, ψ, follow T; the latter, γ, follow τ. The two together are dt = Tdτ which is the overall plessist biological behaviour, λ. This is all so, by definition, and in our model.
All plessists can now act together to form π, thus defining its group of 1s for the doubly closed unipollent equilibrium of plessemorphs, plesseomes, and plessetopes. And … we now have our non-singly dimensioned and irreducible real analytic but biological-ecological set that can suitably interact with the surroundings.
We have also immediately found our Ingredients 1 and 2. They are our Memes 20 and 21. We confirm them by turning to Lev Ginzburg and Mark Colyvan (2004) who inform us that:
• By the Kleiber allometry, an animal’s metabolism has a 3⁄4 power ratio to its mass. If a first animal is 10,000 times larger than a second, its metabolic rate is only 1,000 times greater.
• By the Fenchel allometry, maximal reproduction rate is related to body size through a 1⁄4 power ratio: if an animal is 10,000 times larger, it reproduces at 1⁄10th the speed.
• By the Bonner allometry, maturation time has a 1⁄4 ratio. If an organism is 10,000 times larger, it takes 10 times as long to reach reproductive age.
• By the Damuth allometry, average density in a natural habitat is related to body size. If a mammal is 16 times larger, it has 1⁄8th the numbers per unit area.
• By the Calder allometry, an animal’s oscillation in numbers is related to its body size: an animal 10,000 times larger has a cycle 10 times longer.
Metabolism is therefore proportional to body size, with the total per unit habitat being roughly the same across species. Entities of approximately the same size produce approximately equal numbers, n, of viable offspring so that: “a square mile of horses is the same as the metabolism of a square mile of mice” (Ginzburg and Colyvan 2004).
Our Ingredients 1 and 2 must thus create groups by linking those various hierarchies of times and numbers. They do so as the fibration and cofibration lifts, θ and ρ, to and from our mapping cylinder and deformation retract. And since both of Ingredients 3 and 4 participate in all these interactions, then λ = (ψ , γ, dψ , dγ). Its infinitesimal increments, dλ, lift from the progeny codomain to the mapping cylinder as the fibration, θ; and also from the progenitor domain to the same mapping cylinder as the cofibration, ρ. This is again so by definition.
II.6.4 Elisabeth Lloyd’s (2012) analysis of biological groupings vis-a-vis natural selection, in her Stanford Encyclopedia of Philosophy article “Units and Levels of Selection”, provides a useful summary of these intense and heated debates. Since, at each point in time, t, we must count some n, then we can complete the earlier Memes 14 and 15 by designating t as our Ingredient 1, and n as our Ingredient 2.
II.6.5 Our Meme 22 now declares that as our plessists occupy the successive points τ-1t-1, τ0t0, and τ1t1 on either the Whitney umbrella or the helicoid, they must simultaneously create self-intersections and conversely. We refer to their successive fibration and cofibration states between deformation retract and mapping cylinder as S-1, S0, and S1 respectively. Their average state over the period is S’, and is our deformation retract, being also both the helicoid axis and its middle track. It again immediately involves the ψ and γ quantities of Ingredients 3 and 4 interacting to create the biology and ecology of λ for our plessists and plessemorphs.
If we now refer to the τ-1t-1, τ0t0, τ1t1 and S-1, S0, S1 points more generally, as a, b, and c, then we have everything we need to rigorously describe our plessist behaviours. Since Ingredients 1 and 2 must supervise all self-intersections, helicoids, and fibration, cofibration, deformation retract and mapping cylinder behaviours for our homomorphisms and homeomorphisms, then our Memes 23–29 state the properties they must satisfy so that our plessists can occupy any and all a, b, and c while undertaking the relevant ψ and γ productions involving Ingredients 3 and 4:
I. Identity element. If the circulations are to be recurvatures that complete, then there is always some quantity we can add or remove—such as by dragging the helicoid axis up and down—and that nevertheless leaves things identical. This element or state, S’, must exist. It is both the antipodal recurvature radius and the helicoid axis, and is such that when it is either inserted or removed, every n at every point t any number of generations into either the past or the future looks identical. This S’ must describe a definite self-intersection state and so is a nonzero identity matrix, determinant, or similar. It defines the antipodes and pinch point and the helicoid axis. It is our Hooke cell.
II. Inverse element. Plessists must self-intersect which is to move in opposite directions between one antipodal point, or location, upon our helicoid and another to produce S’. So relative to S’, then for every bigger there is a matching smaller; for every faster, a matching slower; and for every before, a matching after. More generally, for every transformation a in S, there is a −a. This is always a fibration–cofibration coupling. The bare minimum, therefore, is that all points in S are described with rank one tensors with at least two contrasting components—one for ψ and one for γ—attached to each measurement unit to complete a self-intersection … which are then vectors.
III. Closure. If we add, multiply, integrate or differentiate any a and b, we must always get a true and correct value of the same type for our c. Although, strictly, only addition and multiplication are defined as closed, we must still get coherent values for any subtraction, division, and differentiation. Thus if both τ-1t-1 and τ0t0 have S-1 and S0 as an a and a b, then τ1t1 must also exist as S1 and as a c, with the three related as past, present, and future antipodal and helicoid moments and amounts.
IV. Inverse operation. Biology, as a self-intersection, must have an inverse operation. The antipodal pair are inverses. Both addition and multiplication have similar inverse operations which create their identities. The former define subtraction, the latter division: a + −a = 0 and a × 1⁄a = 1. Bringing a vector or tensor together with its inverse similarly creates its identity. A vector’s additive inverse is simply its opposing vector. The inverse of any x is some -x that pushes in exactly the opposite direction, but with the same magnitude. A vector’s multiplicative inverse is a little more involved, for neither dot nor cross products have true inverses. A dot product is a scalar, losing its directional component, and being effectively the shadow length some vector casts in some specified direction. Unfortunately, exactly the same shadow could result by shining a light from some different direction. Similarly, many other vectors could have interacted, orthogonally, to produce any given cross product. But since we demand that succeeding generations repeat, then where one increases, so must others, and by the same amounts. Any x and its successive y must therefore be related so that x⁄y = 1. This immediately means that y⁄x = 1. We can now resolve these matters by noting that the square of any vector is always a positive scalar, with x2 = |x|2 and y2 = |y|2. And since x = y, then x2 = |y|2 meaning x2⁄|y|2 = 1. Therefore every x that completes a circulation will also have, for the multiplicative inverse that creates its antipodal value, its square divided by its absolute value: 1⁄x = x⁄|x|2. These then occupy each antipodal point to create the self-intersecting pinch point and identity, S’, while maintaining all preimages, images, fibrations, cofibrations, deformation retracts, and mapping cylinders. As we did in our Brassica rapa experiment, these can all be easily measured.
V. Associativity. As long as a, b and c maintain the same order, then a + (b + c) = (a + b) + c, and a × (b × c) = (a × b) × c. However, their opposite operations of subtraction and division are not associative so that although 2 + (3 + 4) = (2 + 3) + 4 = 9 and 1 × (2 × 3) = (1 × 2) × 3 = 6, we have (5 - 3) - 2 = 0 whilst 5 - (3 - 2) = 4; and 4 ⁄ (2⁄2) = 4 while (4⁄2) ⁄ 2 = 1. Any vector cross product is also not associative so that x × (y × z) ≠ (x × y) × z. But they nevertheless respect the strict ordering implied by τ-1t-1, τ0t0, and τ1t1. Thus the same inputs lead to the same outputs and successions of states as S-1, S0, and S1 circulation after circulation.
VI. Commutativity. Addition and multiplication follow the rules a + b = b + a and a × b = b × a. However, the opposite operations of subtraction and division are not commutative: 0 - 1 is not the same as 1 - 0, and 1⁄2 is not the same as 2⁄1. Vector cross products are also not commutative: x × y = -x × y. But since there is again a regular sequence of operations, then the same inputs applied in the same sequence at the same locations produce the same states, S, at the same points.
VII. Distributivity. Multiplication distributes over addition so that a × (b + c) = (a × b) + (a × c), with the vector cross product also being distributive so that x × (y + z) = (x × y) + (x × z). If S is some function, ƒ, composed as ƒ(a + b), then we can equally well describe it as ƒ(a) + ƒ(b). An original can therefore distribute itself over many successors. And if some operation is composed of the two parts ab, then its differential d(ab) is adb + bda. So if some successor is composed from the distinct inputs of its predecessor, then the same will hold for its own successors.
II.6.6 We must still account for interactions, λ, with the surroundings. But we have nevertheless defined our recurvatures as plessist reproduction. They are Abelian infinite cyclic groups and subgroups. The group operation involves ψ and γ as quantities of Ingredients 3 and 4. These are added and/or removed as inverse operations with the surroundings within our self-intersecting “biofield” upon our Whitney umbrella and helicoid. This recurvature involves both of the radiative and coupling components; both of the progenitor domain and progeny codomains; and both of the biology and replication globes. The transactions are expressed as fibrations and cofibrations, θ and ρ, and so as the biological interactions, λ, transitioning between preimage and image. The quantities defining S’ are ψ and γ, with the processes sustaining them involving dψ and dγ to give λ = (ψ , γ, dψ, dγ). Those total operations oversee both the homomorphisms and the homeomorphisms. Their productions are the replications not just of biological structures, but also of the biological spaces that are the biology and replication globes, again as infinite cyclic groups and subgroups.
II.7.1 When we take (a) the self-intersection radius, and/or (b) the helicoid midpoint arrow pointing upwards of T; and also (c) the self-intersection boundary, and/or (d) the right helicoid formed by the median equatorial white line of τ; then all populations recurve by hovering about the equilibrium state, S’, using the range ±dS to traverse the necessary intervals. That self-intersection boundary and its equivalent journey about the right helicoid are jointly a replication and a reproduction. They involve both of our biology and replication globes.
II.7.2 Our helicoids, deformation retracts, mapping cylinders, and self-intersections plus antipodal points are all neighbourhood properties. They are therefore topological.
Colin Adams’ The Knot Book offers topology’s standard definition. Figure 10 sets out the well-known intuitions:
Topology is the study of the properties of geometric objects that are preserved under deformations. … we think of the more general geometric objects in topology as deformable. For instance, a topologist does not distinguish a cube from a sphere, since a cube can be deformed into a sphere by rounding off the eight corners and smoothing the twelve edges (Adams 1994).
Topology therefore deals with well-defined geometric objects that surrender some, but not all, of their properties. Topology is still enough like geometry for the objects in the lower two rows in Figure 10 to be three-dimensional. Objects on the bottom row, however, are different in a way geometry regards as insignificant. They are “genus-one” objects with a “hole” and a single “handle”.
II.7.3 Meme 30, displayed in Figure 11, goes on to take ready advantage of topology’s pictorial dimension to advance our model. Since we must carefully consider the different topological properties of all surfaces and interiors, being related as Vn and Sn-1, then that complete figure that supports our recurvatures is more technically a “rotahedron”. The lady is walking about a complete recurving wind wall. She is therefore traversing the radiative–cum–circulating neighbourhoods of our biology and replication globes. This creates both the self-intersections and the circulations of the generations.
By Meme 31, we have a general principle. Any Sn surface supporting a recurvature is homomorphic. It establishes the syntax and structure. It then surrounds a Vn+1 interior that is homeomorphic. That governs the semantics and the space.
II.7.4 As topology suggests, the rotahedron’s S2 recurving surface is, locally, a “two-dimensional manifold”. It is an S2 “plane”. So in spite of the rotahedron’s curved external appearance, its S2 surface is always, locally, infinite and flat, being identical to an ever-extended rectilinear Euclidean plane. The surface is a complete topological “sphere” that supports parallels and unchanging, fully collinear, “affine transformations”. It preserves all angles, ratios, and distances. It has a completely flat “local topology”. Number duples such as (a, b) fix its coordinates. So if one dimension is A, and another B, then all points upon S2 are the Cartesian product A × B = {(a, b) | a ∈ A and b ∈ B}. Its production rules declare the syntax that create that local topology for its exterior.
Although the S2 plane is locally flat, and a plane biosurface, by Meme 32 it simultaneously has the curving “global topology” that wraps it around a V3 rotahedron. That outer S2 sphere therefore bounds a curving biovolume described with three coordinates as a, b, c where A × B × C = {(a, b, c) | a ∈ A, b ∈ B, c ∈ C}.
The interior is a curving V3 “realmspace”. This joint S2–V3 plane–plus–realmspace rotahedron is a rigorous topological manifold. Its production rules declare the semantics and the interior that then create the above syntax and exterior.
II.7.5 By Meme 33, the lady walking about the rotahedron is measuring her circulation, which is both a self-intersection and the recurve journey about the helicoid axis. She is measuring wind walls and her positions for x and y using the method Newton first derived when he solved the problem Johannes Kepler had posed (Hughes-Hallett et al, 2002; Stewart, 2003).
Newton described planetary motion trigonometrically, stating their angles via their side lengths, x and y. He thus used a set of spherical IJK axes, based on a centre x’–y’, and a radius, r. Each point is an x⁄y, and so a ratio between two sides. When those values repeat then an orbit—or in our case, a self-intersecting circulation of the generations, τ—is complete. Looked at in two dimensions, that orbit is a constant acceleration about that x’–y’ centre.
But since Newton also described planetary increments infinitesimally, as dx and dy, he was always dealing with dx⁄x, dx⁄x’, dy⁄y, dy⁄y’, and dx⁄dy. He had thus realized that every infinitesimal increment, dτ, over each infinitesimal time interval, dt, declares its precise sequencing of locations in the circulation as some dτ⁄dt. If these again repeat, a circulation has been completed. And since every dx and dy at any present instant dt0 and dτ0 is added, in each succeeding moment, to its generating x and y, then every increment in some prior dt-1 and dτ-1 becomes a part of x and y in a succeeding dt1 and dτ1. They together define the x’–y’ centre. Therefore: referencing any property to its current state, and so as dx⁄x, immediately uses Newton’s spherical dτ–dt and IJK axes.
II.7.6 Meme 34 is to note that as the lady circulates across each x and y in each of the rotahedron’s distinct X and Y hemispheres, she is also always (a) somewhere about the central point S’; and (b) somewhere between an initial and a final hemispherical location. But a line from every x passes through S’ at the centre—which is the identity—to emerge in its antipodal y. There is therefore a V3 or Euclidean 3-space or realmspace composed of all lines passing through that origin. Each such line is a unit vector pointing in a given direction. It is opposed by another pointing to its antipodal point. We thus have a unit rotahedron that forms the unit Eulerian limits for any circulation.
II.7.7 For Meme 35, our unit rotahedron abides by Bezout’s theorem. This states that any two planar algebraic curves of degree n and m intersect in exactly mn points. Any two circles therefore intersect in four points: two real, and two upon the “line at infinity”. The rotahedron’s horizon is therefore at that line at infinity, therefore making all points upon it “properly countable”.
By Bezout’s theorem every generation or orbit about the population is in fact a circle that passes through the properly counted point at infinity … which is also our replication point. The “antipodal map” is therefore the identification of each opposite point. It creates our self-intersection. Both the replication point, as θ–ρ, and the Möbius strip boundary between the biology and replication globes that define the passage from one generation to the next forwards as ‘×’, and backwards as ‘÷’ are such self-intersections. Every population can therefore replicate infinitely many times, leaving the original unchanged.
Since, for Meme 36, the S2 plane is a two-manifold whose local topology reaches out to infinity, then granted that each antipodal point is “over the horizon”, and so “out of sight”, by Meme 37, the fibration and cofibration act through the deformation retract and mapping cylinder to recreate each antipodal point as the equally properly counted point beyond infinity.
II.7.8 The succession all around a circulation as the lady walks about the rotahedron is the key to the recurvatures that are the generations. The resulting spherical axes measure both the biology–replication heredity and the temporal passing of a generation. Both are measured as the ongoing and bounding circulation, τ, of definite radius, r … and also as the absolute time, T. We therefore have both the radiative and the circulating—and all their transformations—for the fibration and cofibration.
II.8.1 If we wish to reckon both the biology–replication interface for the Möbius strip, and the temporal interface that marks the beginnings and endings of the generations, then we must ensure that all neighbourhoods remain intact. We must ensure that all distances about the rotahedron’s surface for its local A × B topology match those across the centre for its global A × B × C topology.
II.8.2 We now consider, for Meme 38, the two commandos in Figure 12 running about a rotahedron. We also recollect that Memes 4 to 9 placed our plessists and/or plessemorphs a1 and aa into our first set A; their plessiomes and/or plesseomes b1 and ba into a second set, B; and their plemes and/or plessetopes c1 and ca into a third set C. They involve the infinite cyclic groups that are our biology and replication globes, as well as our deformation retract and mapping cylinder.
The commandos’ fibrations and cofibrations as they run about the rotahedron and navigate between A, B, and C are the transitions between some initial point α0 and some final point F, as preimage and image, being (a-1, b-1, c-1) → (a1, b1, c1) and (aa, ba, ca) → (ab, bb, cb) for, respectively, some plessists and plessemorphs. They are each statements in a Chomsky grammar. They are both homomorphisms and homeomorphisms.
II.8.3 For Meme 39, our two commandos are impelled by forces that pull them away from their initial basepoint, α0. Since we are interested in both a set of Chomsky production rules and their biological effects, then these are the same ψ and γ forces that produce the more general λ and DNA-based infinite cyclic group and homo- and homeomorphisms, as transformations in nucleotide codons, in the humanoids underneath.
We let the commandos have all the ropes, speedboats, all-terrain vehicles and etc. they need to navigate the terrain … meaning they are free to interact with the surroundings as they wish. We attach elastic strings and sheets to their hands, feet, and head. They therefore draw a whole series of lines, surfaces, and volumes to create our self-intersections and helicoids as statements in the general syntax and semantics. We can measure both the radiative and the circulating forces working on them—which create our fibrations and cofibrations—by their external effects upon those attached elastic strings and sheets.
For Meme 40, we confirm that our radiative force is composed of Meme 18’s Ingredients 3 as ψ. Somewhat like a pod of whales migrating towards colder temperatures, it pulls Commando 1 due north.
And we confirm, for Meme 41, that our circulating force is composed of Meme 19’s Ingredients 4 as γ. Somewhat like plants sprouting leaves under increasing sunlight, it pulls Commando 2 due east.
II.8.4 We need the velocities all about those wind walls. So reporting our two commandos as travelling with a simplistic velocity or rate of change—i.e. rate of change of distance—upon the underlying surface, and so as at so many kilometres per hour, is not helpful. This only uses the standard rectilinear ijk axes of this ordinary surrounding three-dimensional Euclidean realm. So for Meme 42, Commando 1 notices that when he examines the northern and southern faces of his little surrounding box of volume elements, then bigger values for latitude keep coming at him from the north as +dψ … while smaller ones keep departing him to the south as -dψ.
James Maxwell (1870) was the first to apply the term “convergence” to this realm or volume phenomenon; with William Kingdon Clifford (1878) being the first to apply its opposite of “divergence”. A divergence is thus some property’s increasing rate of change, but directly in alignment with its applicable field of force. Therefore, this Meme 42 says that Commando 1 currently has a “positive divergence”, dψ, in the radiative force, which is for latitude. It is the main cause of fibrations and cofibrations—and so contributions to the mapping cylinder—along that given axis.
And since Commando 2 is similarly travelling in a direction aligned with his alternative field of force, then for Meme 43 he similarly sees increasing longitude values, +dγ, again in terms of the underlying surface, coming at him upon his eastern edge of his volume elements; with smaller ones disappearing, as -dγ, to his west. Since this is similarly aligned with the impelling force, Meme 44 says that he currently has a positive divergence, +dγ, in that circulating force for longitude. It is thus the main cause of fibrations and cofibrations, and of mapping cylinder activities along its given axis.
II.8.5 Each commando will of course have to move around obstacles. This requires deviations into and out of each other’s directions … which means movements that either add to or subtract from the velocities and accelerations that they each currently have, courtesy of their circulating wind walls.
We now follow the convention Maxwell established (1870). He originally called these recurvature and wind wall transformation phenomena ‘twirls’, but the modern designation is “curl”. So Meme 45 says that each commando can curl—but in this case only two-dimensionally—directly into the other’s directions. Each can therefore change their wind wall velocities and behaviours so they align, at least temporarily, with the other. It is to each as if each has temporarily been placed under the purview of the other one’s force; and so is blowing slightly in that other direction, exhibiting a suitable change in both velocity and wind wall behaviour. That makes each one more or less like the other, by reshaping their wind walls in that direction.
II.8.6 There is, of course, a further consideration. John Ambrose Fleming regularized these interactivities. Since a curl is any rate of change at right angles to a given applied force, then by Fleming’s right-hand rule, our meme is that every time a commando goes rightwards, he registers a positive curl. So all deviations eastwards by the radiating force for Commando 1, and southwards by the circulating force for Commando 2, are each positive curls in longitude and latitude, respectively. These are both positive contributions—+dγ and +dψ—to the mapping cylinder; with their leftwards movements therefore being negative. Each thus also contributes to the overall fibration, cofibration, homomorphism, and homeomorphism and their joint general biological effect, λ.
II.8.7 Each commando will additionally go up and down hills; and down and up valleys. These are curls, by both, into some third dimension. They are further contributions to λ, and so to the mapping cylinder. As fibrations and cofibrations and infinite cyclic subgroups, they add to or subtract from the overall movements upon the mapping cylinder between the biology and replication globes, which are the infinite cyclic groups.
II.8.8 Again by Fleming’s right-hand rule, when forces, fibrations, and cofibrations combine to decrease height while keeping a locally lowest point to the right; or else to increase it by keeping a locally highest point to the left; then that is a positive curl for height and so is +dλ, with the opposites being negative, -dλ. Thus Meme 46 declares that to cross a hilly incline up and then down, or a valley down and then up, but always keeping the local maximum on the same side, produces a net curl, into the third dimension, and for that obstacle, of zero. The wind wall overall maintains the same height and direction of motion.
II.8.9 We now only need to distinguish homomorphic or structural transformational effects from homeomorphic and spatial ones as between biology and replication globes. We also need to clarify all movements into that third dimension that create the heights and depths—and so vertical velocities—upon these circulating wind walls.
II.9.1 We have a variety of biological and DNA interactions. Some incorporate the replication globe; some do not. If want to understand the effects of these ±dψ and ±dγ curls that contribute to dλ, then we must measure all volumes and surfaces, energies and momentums, and fibrations and cofibrations. We must determine all the productions as transfers to and from preimages and images that occur in our self-intersections, helicoids, and rotahedrons.
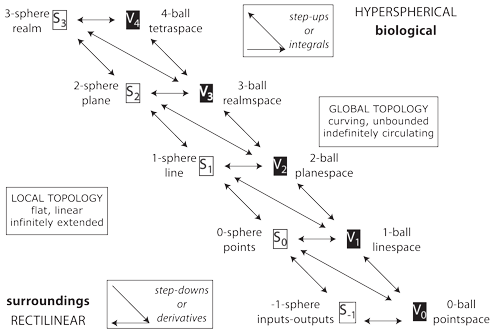
II.9.2 Figure 13 illustrates Meme 48, which is the emerging biological grammar for the language spoken by those curls and their resulting biological transformations. That grammar confirms that as the commandos run, they create a set of hyperspherical biovolumes, V, with their elastic sheeting. Each resulting biovolume presents its cylindrical biosurface, S, to the surroundings. If the volumes are (A, B, C), then the surfaces are ((A, B)C, (A, C)B, (B, C)A) where a is in A, b is in B, and c is in C; and where each is held as a specific direction of observation, the others then being varied. The surfaces are the three different perspectives—one in each of the A, B, and C directions—that create the whole.
II.9.3 Another aspect of our grammar is that the external world does not, itself, connect any elements upon the left of Figures 1 and 13 to create any structures to the right. The external world has no λ or recurvature process. All λ connections are exclusive to recursive functions; to our running commandos; and so to all biological entities. Therefore, only the biovolumes V0,1,2,3,4 displayed on the right can recurve. They are intrinsically biological; are hyperspherical; contain the energies and semantics; and are homeomorphisms. They have an extra global dimension and can exert a semantic pressure per unit volume throughout their relevant space.
Their energies are then incident upon the surroundings, to their left, emerging as lower-dimensioned cylinders and loops—and so as discernible events—through the relevant S-1,0,1,2,3 surfaces. Those are their outward expressions as biological events per unit surface, and so are their syntactical structures and homomorphisms through Ingredients 2, 3, and 4.
II.9.4 Our main interest, in Figure 12, is in the two humanoids underneath the two commandos. Since we want to distinguish their homo- from their homeomorphisms, then Meme 47 is to instruct the commandos to give each other personalized renditions of their ongoing transformations, using their walkie-talkies. Each commando is, for example, to report his own progress, and his observable effects on their linking elastic sheet, to the other in terms of his own distinct “height-lengths”, and as measured directly upon that surface and sheet.
We note, for Meme 49, that since our commandos are equipped with all necessary accessories, then we can switch them and/or the forces around at any time. Where one goes, the other could equally well go. Granted that the Greek for ‘place’ is topos, then they are “homotopically equivalent”.
So for Meme 50 then after one day, the forces switch so that Commando 1 is instead being pulled due east, by γ, with Commando 2 being pulled due north by ψ. Since they are homotopically equivalent, then we let them meet up at the end of that second day, at F, to create a “Levi-Civita parallelogramoid”.
II.9.5 We now have a complete set of production rules. The commandos both understand both. They are homotopically equivalent. But even though in many ways equivalent, we cannot just assume that they are perfectly substitutable.
We can perhaps better understand their limitations by understanding the continuities involved. We can compare these commandos, and the forces acting on them, to the letters ‘X’ and ‘Y’.
The letters ‘O’, ‘A’, ‘D’ and ‘B’ all have holes. Although X and Y are similar in both being without such holes, the Y has a single ‘three-vertex’, the X a single ‘four-vertex’. The X can deformation retract onto the Y because we can retract one of its prongs to another. But we can also deformation retract three of the X-prongs onto the three in the Y, and then retract X’s fourth to Y’s centre. We can even retract each prong in each letter to its own centre.
We can next remove both centres. The X now yields four components, the Y only three, all again without holes. All paths in each can continuously deform into each other and retract to a point, always remaining within its component. All seven components are therefore “simply-connected” and homeomorphic. Nevertheless, the original X and Y are not homeomorphic. They are, however, homotopically equivalent.
II.9.6 The mapping cylinders our commandos interact with can similarly have different possibilities. We must find a way to guarantee that they are not merely homomorphic, but also homeomorphic.
For Meme 50, we note shapes A, B, and C in Figure 12. They could easily be the elastic shapes our commandos construct. But although all such shapes class as homotopically equivalent, we observe that no matter how Euclidean they might appear locally, when looked at globally, no true straight lines, rectangles, or parallelepipeds can exist on any sphere. The commandos will not necessarily create matching “squaroids”.
The commandos’ paths will only properly match if the terrains they cover straddle both the equator and the prime meridian on the same surface, and so that they are properly reflexive and identical. So while everything homeomorphic will immediately be homotopically equivalent, the converse is not necessarily so, for not everything homotopically equivalent is homeomorphic.
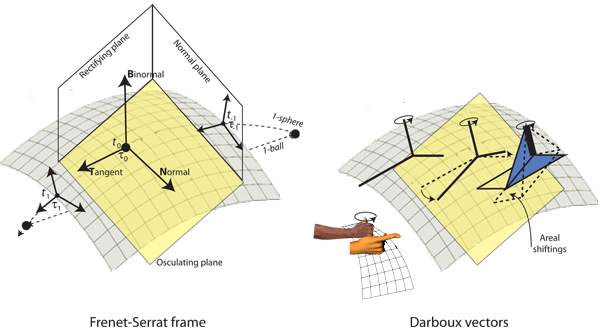
II.9.7 As in Figure 14 the French mathematicians Jean Frédéric Frenet and Joseph Alfred Serrat discovered, independently (Crenshaw 1993a, 1993b; Crenshaw, H., Edelstein-Keshet, L. 1993; Crenshaw, H., Ciampaglio, C., McHenry, M., 2000), that we can blend Newton’s IJK hyperspherical axis system with the ordinary tangential and rectilinear ijk one to determine whether or not our shapes are homeomorphic. The two ijk and IJK axes can establish both a “1-sphere” and a curved line, dτ, for its linespace and circulation. But we can also use the axes and any resulting curve to determine a tangent, T, by taking the derivative. It is the shortest path between the points we are measuring. It is the tendency for any curve to depart from a straight line. It is formally known as a “1-ball”.
We can, however, take yet another derivative to that derivative. That double derivative establishes the normal, N, and tells us how the tangent itself is changing, which is its acceleration. The normal points straight at the centre of any curvature.
Since the tangent and the normal are mutually orthogonal, they form a plane tangential to the original surface, just touching it at that point. Gottfried Leibniz first used the Latin term osculans, ‘kissing’, for this behaviour. It is therefore called the “osculating plane” (Howard 1992). It tells us the rates of left-right arcing, twisting, and turning.
The third dimension we require, to properly analyse ψ and γ, is orthogonal to the two we already have. It is therefore easily calculated. It gives the binormal, B. When we bring normal and binormal together, we create the “normal plane”, orthogonal to the osculating one. We can now measure “torsion”, the surface’s accelerations up into, or out of, the osculating plane as we go right-left. We can now assess the effects of dγ on dλ.
We can finally bring tangent and binormal together to create the “rectifying plane”. It tells us how much the surface lifts towards, or drops away from, the binormal as we travel forwards-backwards. We can now assess the joint effects of dγ and dψ on dλ.
II.9.8 Shortly after the French mathematician Jean Gaston Darboux learned about the “Frenet-Serrat trihedron” or “Frenet-Serrat frame”, he realized that although it describes all translational movements, it misses all rotating ones. If, as in Figure 14, we twist the thumb upon the binormal, the tangent and normal curl to different directions. Darboux noted, however, that they are linked. The rotated index finger is still orthogonal. There are therefore matched exchanges. Again by Fleming’s right-hand rule, if the osculating plane moves counterclockwise to push the normal towards the binormal, or clockwise to push it away, that is positive; otherwise it is negative. The areal velocities on the osculating, normal, and rectifying planes now state all curls.
We now have every parameter, in every neighbourhood, and upon any surface, through all transformations wrought by our raying and circulating fields … which create the fibrations and cofibrations to and from our mapping cylinder. Thanks to the Frenet-Serrat trihedron, even the most tortuous of mapping cylinder surfaces become locally straight lines and flat surfaces, S … but we still always know exactly how much they might be moving curvilinearly as V. We can soon observe, for example, that although the earth has a local two-dimensional and (A, B) topology that makes it appear flat everywhere, it nevertheless curves about itself with a global and three-dimensional (A, B, C) topology that has an average rate of curvature of 13 centimetres per kilometre. We can determine this by observing each of the local (A, B)C, (A, C)B, and (B, C)A topologies, which then come together to reveal the global (A, B, C) characteristics.
If we therefore want to determine all curls and three-dimensional variations, which are any extraneous effects ψ and γ may have upon each other and/or upon any third dimension, then our lady and our two commandos must report all values in three different ways:
• Rectilinearly, ijk. These are, simply, their absolute motions emerging tangentially through their surfaces, measured as seconds, kilometres, kilogrammes, and other SI units, being rectilinear and Euclidean. This is Meme 51.
• Hyperspherically, IJK. These are Newton’s values stated proportionately, i.e. with respect to their running totals, and so as dx⁄x. They are recurvature values equivalent to radians per second about the earth. They complete a generation about some x’ centre, in terms of related antipodal values, and centralized, continuous, hereditary behaviours. This is Meme 52.
• Frenet-Serrat TNB. These state the surface directly in terms of current biovolume interior elements, such as via height-lengths, or whatever and other individualized and relevant properties of interest. We already have this as Meme 47.
Those are then the distinct perspectives upon each of (A, B)C, (A, C)B, and (B, C)A, which then come together to reveal (A, B, C).
II.9.9 As in Figures 1 and 13, any two S0 values or points immediately form a biosurface, linking as a V1 biovolume and linespace of definite value. So in accordance with our Meme 48 grammar and our Figure 8 Whitney umbrella, each distinct S0 point our two commandos pass through has a structure. It is in fact a combined Sn-1–Vn. So our S0 point is fact an S-1–V0 pointspace. It has its radiative and circulating couple as a -r and +r input-output pairing. Those together create a direct and tangential V1 1-ball which is a linespace. There is an independent linespace in each of A, B, and C.
And also, just as a terrestrial road can deviate and lengthen a journey, any two S0 values or points can be linked by varied accelerations and velocities in our windwalls and recurvatures about the rotahedron. That curving S0 is the route the commandos would actually have to take, upon the surface, to get from one point to the other. We designate this curving 1-sphere line ‘S1’.
Meme 51 therefore states that between any two points S0, there is:
• a V1 biovolume as a direct linespace; and
• an S1 biosurface as lines; and that is composed of
• the specific input-output points -r and +r that create them.
This is our complete S0–V1 nonpollent and production rule pairing as syntax and semantics.
And then as a general principle, two S1 relationships or curves can bound an S2 plane or area that, no matter how convoluted, can also be expressed as a completely regular V2 “rotagon”. This is the combination of bounding circle or circumference, at radius r, plus its enclosed “disc” of so many square metres or relevant units. Therefore: between any collection of values as S1 lines, lies a V2 rotagon as their coordination. It is a given “planespace” and biovolume for our similar S1–V2 unipollent production rule and syntax–semantics pairing.
In the same way, any given S2 planes, of whatever shape, can bound a rectilinear S3 realm or volume. And no matter what its complexity of surfaces, there will be a uniform V3 rotahedron of radius r whose surface and interior ball summarize a three-dimensional realmspace as so many cubic metres, or the equivalent, for our S2–V3 pluripollent pairing.
And by the same token, two or more S3 realms are related via a V4 “rotachoron”. This is a four-dimensional hypersphere again of definite radius, volume, and properties. Its surface is a set of S3 “glomes”. Its interior is a V4 “gongyl”, creating our S3–V4 totipollent pairing.
II.9.10 Since the rotachoron is a four-dimensional hypersphere, then its set of three dimensional bounding glomes circumscribe a set of S0 = -r and S0 = +r pointspaces equidistantly about its centre. We always get a mean value for ψ and γ. These establish the λ of biological-ecological behaviours for our archetypal plessemorphs, and their plesseomes, and plessetopes.
Our rotachoron’s four dimensions now have the same two solutions all about themselves, based on ±r. Since its shape is symmetrical, its internal V4 volume or gongyl is given by dr = 0, and ∫dr = 0. And while that V4 interior biovolume cares only that all its circulating points, τ, stay equidistantly about it at r, the external surroundings will allocate them a set of real-world values according to distance and orientation as +r and -r. Meme 53 now says that one in each such pairing, -r, is a net output from our plessists and biological events to the surroundings; the other, +r, is a net input to our plessists and plessemorphs from those same surroundings. We have the syntax and semantics that create the recurvatures.
II.9.11 These above processes are of course more technically called “integrals” and “derivatives”. But as in Figure 13, our Meme 48 grammar calls them “step-ups” and “step-downs”, respectively. We step down from (A, B, C) to (A, B)C, (A, C)B, and (B, C)A; and we step up from them back to (A, B, C). So we can step-up from a one-dimensional figure to a two-dimensional one, such as when pick up a line, x, and push it a certain distance y across a plane to create an xy square; or take up that xy square and push it along the same line for the distance z to create an xyz cube. Step-ups then determine—as does the integral calculus—overall totals as distances, areas, volumes etc. and creates Vn biovolumes. Step-downs then do the opposite. They determine how things have changed to create those step-ups. They find all related, surrounding, momentum interactions as Sn-1 biosurfaces. As in Figure 1, we again have the syntactic and semantic interactions, as spheres and cylinders, that sustain all biological entities.
II.10.1 We must now very carefully consider our two commandos, who represent all biological interactions with the surroundings. They are homomorphic, meaning they are immediately homotopically equivalent. Since we can switch them around at any time, then if one is P and the other Q, Meme 54 recognizes that their joint PQ mapping cylinder satisfies their joint fibrations and cofibrations. Both of their preimages and images map to their joint mapping cylinder. Their joint image is their joint deformation retract. Their joint preimage uses their joint identity—which is some S’PQ—to reach that joint mapping cylinder.
II.10.2 But unfortunately, our commmandos will most probably have different rates of change. Their boundary transformations, formed by running, are unlikely ever to be the same. Indeed, since they both feed into the same mapping cylinder—which is simply the surroundings—then that mapping cylinder will always contain a greater number of transformational possibilities than does any distinct preimage or image lifting to it. There is therefore no necessary guarantee that any preimages and images are identical. We indeed confirm, for Meme 55, that shapes A, B, and C in Figure 12 need not be homeomorphic, and do not automatically create true squaroids. Our two populations can combine in very different ways every time.
II.10.3 For Meme 56 we now let a single commando run the entire circulation from α0 to F and back to α0. This is a complete syntax and semantics and recurvature. The humanoids underneath do the same.
II.10.4 Although we now have our circulation of the generations, we still have no guarantee that any two such circuits are homeomorphic. But since species certainly exist … then some wind wall transformations and recurvatures, and some syntaxes and semantics, must be sufficiently close to others … as, indeed, are the plessists that we have already defined as sufficiently close neighbours. We have to determine the syntax and semantics that could produce such similarities.
II.11.1 We can find our Chomsky production and recurvature rules by returning to Figure 7 where we exchanged the replication point fibration–cofibration transition for a biology–replication globe one as the start of a generation by creating a Möbius strip interaction across our mapping cylinder of the surroundings. But it is quite easy for these two to be homotopically equivalent, but not homeomorphic. Since not all mappings are fibrations, and also since different dimensions are involved, we cannot just assume we have maintained an equivalence.
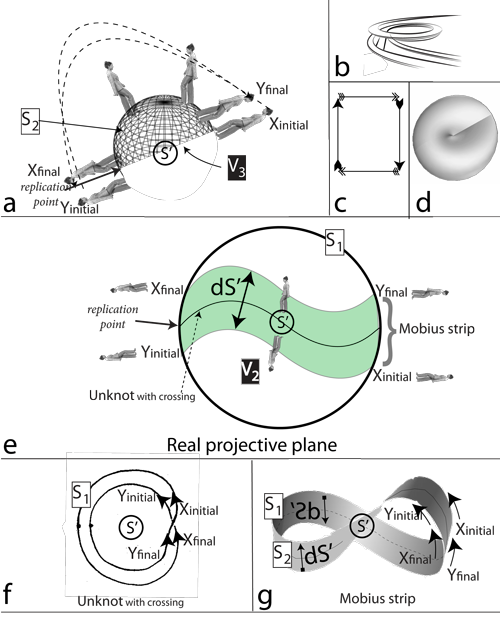
II.11.2 We can apply our burgeoning self-intersection and topological principles to the Meme 57 we see in Figure 15a as the lady walking about the hemi-rotahedron to produce all recurvatures and a circulation.
Since we already have our Whitney umbrella, which contains our antipodal map and self-intersections, then Meme 58 is to note that since we can get every southern journey on the rotahedron from the north, then we have no real need for that southern hemisphere. We can identify it with the northern one. That way, any wind walls that cross in one half, are guaranteed to cross in the other, and produce a circulation.
II.11.3 If we cut a rotahedron in half and flatten it down against a plane, the equator goes steadily out to infinity. Bezout’s theorem nevertheless applies equally well to our new self-intersection, even if it moves infinitely far away. Since the point at infinity is properly counted, then every point in the lady’s northern hemisphere uniquely determines one in the south. All points y in the “missing” southern hemisphere, Y, are therefore identified by some x in her currently visible northern X one.
The identification of opposite points can have consequences for movements proposed in other dimensions. Figure 15b shows what we as three-dimensional beings regard as a perfectly ordinary (x, y, z) movement and recurvature in three dimensions. It is a highway overpass. But it would completely mystify a two-dimensional being forced to move in only x and y. They would instead see varied movements in their two dimensions, from which they might deduce events in a third.
Identifying our biology and replication globes in that same kind of way allows us to investigate the higher dimensioned upsilon–delta recurvatures. They appear to us, in a lower dimensions, as smooth movements across our mapping cylinder. Identifying the fibration to cofibration transition as a lower-dimensioned replication point, as we do with our hemi-rotahedron, allows us to continue smoothly forwards, through λ. We then undertake, and can measure the effects of, a higher-dimensional transition without taking it explicitly into account.
II.11.4 Since the northern hemisphere in Figure 15a is topologically homeomorphic to a V2 rotagon, we can “flatten” it to produce Figure 15e’s planespace. All opposite points are identified.
We now have a sphere modulo the antipodal map known as the “real projective plane”. A journey across our new surface is equivalent to one that does a complete orbit about a rotahedron. It crosses over the replication point. It recurves to be both a circulation and a reproduction.
The band across the projective plane has become the complete journey to the opposite hemisphere and back again … and so is a Möbius strip. We have similarly identified the biology and replication globes. Since this Möbius strip passes through both those biology and replication globes, then it circumscribes a complete generation.
II.11.5 We now have all our self-intersections in all dimensions. Since we have identified the rotahedron’s two hemispheres, every point upon the projective plane is simultaneously (a) some point +r; (b) its antipodal point -r; and (c) a line of diameter 2r stretching between them. The real projective plane is therefore a Möbius strip with a disc attached to its boundary. All lines across it are complete planes formed as parts of the geodesics and great circles linking each other diametrically—again in all dimensions—through the origin.
II.11.6 Although the real projective unfortunately cannot be realized in three dimensions, its “fundamental polygon” in Figure 15c shows how it might be constructed. We first create a Möbius strip by stretching one pair of edges out; twisting them about to make their arrows line up; and then gluing them together. The other two sides are then also stretched out; are twisted so their arrows again line up; and are glued together. That second gluing passes right through the first surface and produces both a complete line of self-intersection and a real projective plane. As in Figure 15d, it looks, in three dimensions, as if it intersects itself, locally. But when seen globally, and in four, it does not self-intersect any more than does the Figure 15b overpass style intersection when observed in three dimensions, and no matter how it might appear in only two when seen by some such lower-dimensioned being. The real projective plane allows us to continue as easily from globe to globe, and so from beginning to end of a generation, as we do across the replication point. The one is equivalent to the other.
II.11.7 The real projective plane is the smallest “nonorientable surface”. It is nonoriented because what currently looks like a journey to its opposite side is in fact a continuous shift, in another dimension, that then continues the same journey … which is in our case the transfer over to the beginning of a next generation.
The real projective plane has an Euler characteristic χ = 1. Its complete line of self-intersection, in Figure 15d, is defined by two pinch points at each end, and is formally called a “crosscap”.
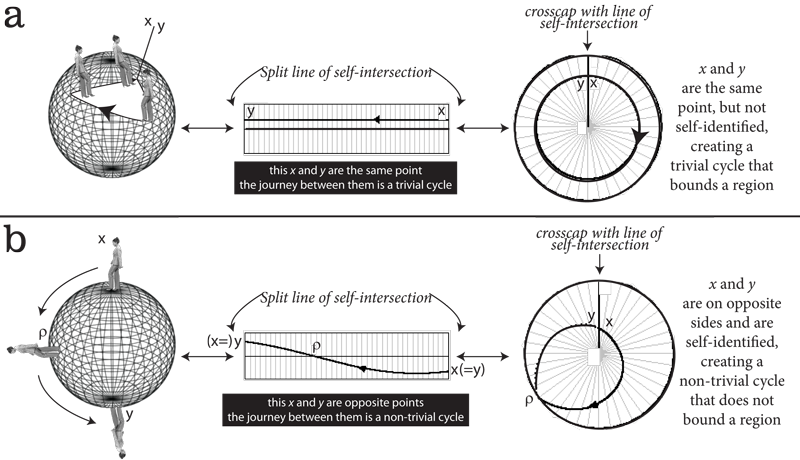
II.11.8 The two points on each edge of a projective plane are identified—glued together—so they are continuous. So also, a journey up a helicoid goes on continuously upwards, yet constantly repeats each point, but always in the next generation. There has in each case been both a fibration and cofibration, which is λ = ψ + γ = q + r.
The points lying on lines upon the projective plane that travel to a boundary have crossed the equator, as the line located at infinity. To again flatten a hemisphere is to push its equator all the way out to infinity; to transition over to the other hemisphere out at infinity; and then to return. But this is the same as simply turning round; going upside down; and returning as if upon the other side.
The points either side of the equator have now been identified. As in Figure 16a, points on lines that do not cross the boundary are not identified, and so are not each other’s antipodes. Thus the lady in 16a does a circuit upon the rotahedron surface. We have x = y on the rectangle next to her. The two border points are the same for they are the same side of the equator. Since she does not cross the equator, the rectangle’s two end points are not identified. The projective plane on her far right shows her trivial cycle. It bounds a region and returns to the same point. The rectangle’s midline and the projective line’s boundary are that equator. She makes no contact with either.
II.11.9 The lady’s journey in Figure 16b is different. It crosses the equator at ρ. The points x and y are therefore identified. The path on the rectangle shows that equatorial crossing identified. The x and y are the same. But y is x’s inverse, for she is now upside down on the other side. The path over on the projective plane now touches the boundary to show that the lady has walked some great circle.
II.11.10 Each point upon a projective plane is combined with its antipodal one located at 2r. The journey across it traverses both a rotahedron’s halves, looping about to return to its beginning. Therefore, any curve starting on a projective plane’s identified line that crosses over to its opposite point forms a curve touching the boundary that is immediately a complete circulation of the generations. It involves reproduction. All curves not reaching from boundary to boundary are trivial cycles within one or another hemisphere and/or globe. Those do not pass the replication point or initiate a generation.
II.11.11 Meme 59 is now to point out that we have our reproductive cycle. Evolution has become a pure exercise in topological reasoning. Our biological self-intersections, fibrations, cofibrations, and biology and replication globe transitions now occur completely naturally, and in whatever dimension.
II.11.12 We also now have a way to distinguish the biological from the non-biological, and biological trivial cycles from non-trivial ones. We can use a sphere for the trivial, a torus for the non-trivial that can cross an equator, and the real projective plane to establish maxima and minima for those that can do both.
II.12.1 The ability to flatten an entire surface from an (x, y, z) to each of
(x, y)z, (x, z)y, and (y, z)x, and then to step back up again to (x, y, z) is certainly an advance. But if we turn to four dimensions, which are then (x, y, z, w), then when we flatten, the w events will have some shadow or presence in (x, y, z)w, even if it is only in the fact that we look constantly in that direction. The same goes for the others. And if we retract further to consider only x, and y, then the w and z will still have some kind of presence in the resulting (x, y)zw. Flattening nevertheless places whatever recurvature motions occur in our given direction of interest firmly upon that two-dimensional plane. Studying all of the (x, y)zw, (x, z)yw, (x, w)yz, (y, z)xw, (y, w)xz, and
(z, w)xy planespaces and perspectives allows us to reconstruct the entire four dimensional (x, y, z, w) global behaviour.
Meme 60 uses Figure 17 to point out certain topological identities. When that rotagon is examined infinitesimally closely, then:
1. its bounding “unknot”;
2. Figure 15f’s “unknot with crossing”;
3. the edging or boundary to Figure 15e’s Möbius strip;
are all the same. Meme 61 then confirms that all three lines and/or linespaces can be produced by—and indeed are—“one-manifolds” that help establish these different perspectives. There is a similarity in that all six of the above planespaces we produce by flatteninng are V2s with an S1 bound.
II.12.2 If we take what we have learned from the real projective plane, then by Meme 62, of Figure 15g, the neighbourhood all about an unknot is a nonorientable Möbius strip. Its +x attributes identify with their -x opposites to declare a given biological circulation. Plessists and their properties of greater and lesser lying on one side of any self-intersecting point will each promptly lie as their opposites of lesser and greater upon that opposite side. And as their attributes suitably invert from one subpopulation or side of the Möbius strip to the other, they create their joint S’; the complete circulation; and the fibration–cofibration lifting to a mapping cylinder. That is the defining plessemorph, plesseome, plessetope interaction. It is also the unknot with crossing in Figure 15f; which is the edging to the Möbius strip in Figure 15g; and the right helicoid in Figure 9.
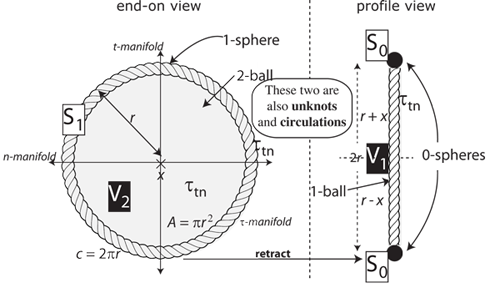
II.12.3 Figure 17 confirms, through Meme 63, that our recurvature on a rotahedron is an S2 biosurface event on a V3 biovolume that can always be “flattened”. All opposite points again identify. The flattened whole becomes a V2 rotagon with its S1 bound. The journey to the opposite side and back is a line across the surface.
II.12.4 Meme 64 now notes that Figure 17 is specifically created from our Ingredients 1 and 2 of t and n, to make τtn. Its bound can then act both recti- and curvilinearly, as both line and linespace in both time and number over a circulation. This simply means that we can always count n of our chosen artefacts at each moment, t.
This same meme further notes that t and n form (a) the internal τtn planespace as biovolume, V2; and (b) the bounding τtn S1 line, as the biosurface, S1. This S2–V3 flattening therefore gives our S1–V2 rotagon. The meme concludes by noting that such S2–V3 to S1–V2 flattenings are equally possible for the t and m, t and p, n and m, n and p, and m and p couplings, making six in all.
II.12.5 By Meme 65, the S1–V2 rotagon we have produced above is also an unknot. Since, for Meme 66, it can shrink to a point, it is simply-connected. This flattening of an S2–V3 rotahedron therefore again gives an S1–V2 rotagon of various dimensionalities.
II.12.6 For Meme 67, we confirm that the rotagon we produce has an S1 circulation with the global topology of a circle … but the local topology of an infinitely long straight Euclidean line, for that is always how it appears when viewed infinitesimally closely. That bound is a distinct 1-sphere, with Figure 17’s again being the conjoined one-manifold, τtn. It therefore gives us both time and number for T and τ for our helicoids and self-intersections, with T being absolute and rectilinear, and τ stating the relative distance between the beginning and end of a generation.
By Meme 68, our V2 rotagon, bounded by its S1 surface, can also retract. As on the right of Figure 17, we can observe it in profile. That is a further flattening. It again brings properties together.
II.12.7 The V2 disc’s profile is a step-down V1 linespace with S0 endpoints. It is the linking V1 line, stretching between (r - x’) and (r + x’). Our V2 rotagon’s biovolume, and planespace, therefore present an S1 biosurface, and line, to the surroundings. The enclosed V2 area is the integral of the S1 presenting biosurface; while the S1 line is its circumference and derivative. So by Meme 69, our S1, also made from t and n, is simultaneously the contained V2 planespace’s derivative. By Meme 70, that line’s biovolume is V1 = 2r, the step-down derivative. The same holds for all others.
II.12.8 Then by Meme 71, our S1 biosurface can also further retract. We can view that line end on. It has two different profiles, one for each end. This gives the two S0 end points with specific values for t, n, and all others.
Since we now have a further retraction, and step-down derivative, then the two S0 end points taken together are technically the “0-sphere”. They are our V0 with its -r and +r pointspace, separated by 2r. When pulled apart and suitably joined with others of their kind, they have the syntax and semantics to construct our V4 rotachoron.
II.12.9 And then further since, by Meme 72, that V0 pointspace covers the S1 line and/or linespace’s ends, then the two together are its surface area, such that S0 = 2. And those are again the -r and +r inputs and outputs. These build our V4, and so our biological population, from progenitor domain to progeny codomain. They use the Chomsky hierarchy and this biological grammar of surfaces and volumes which are the recursive functions and infinite cyclic groups and subgroups that build our wind walls and recurvatures.
II.13.1 If we are to be properly biological, then we must build those wind walls and recurvatures. We must also reconcile the homomorphic, the homeomorphic, and the homotopically equivalent, and properly account for our infinite cyclic groups and their subgroups. We therefore return, for Meme 73, to the four levels Lloyd discusses (2012). They must create the symmetries that can replicate and recurve.
II.13.2 For Meme 74, we turn to Wilson, who confirms the assignments of our four Ingredients to given biological effects:
Biology is a science of three dimensions. The first is the study of each species across all levels of biological organization, molecule to cell to organism to population to ecosystem. The second dimension is the diversity of all species in the biosphere. The third dimension is the history of each species in turn, comprising both its genetic evolution and the environmental change that drove the evolution (Wilson 2005).
We thus categorize our four one-manifilds of τt, τn, τm, and τp as follows:
• Ingredient 1 is t and works largely at the population level, sequencing entire groups of our plessists into generations, through τ to give τt.
• Ingredient 2 is n and arranges and maintains the cells that form the n entities in any population, but also counts all λ constructs built jointly by ψ and γ in the infinite cyclic subgroups that act over t as the λ biology to give τn.
• Ingredient 3 is p and mostly arranges molecules into cells; but also provides all energy to build base-pairs into nucleotide codons and the like. It is at the heart of our Chomsky-style semantics, and contributes to ψ. It gives τp.
• Ingredient 4 is m, the molecular nucleotide and DNA count. It is at the heart of our Chomsky-style syntax and contributes to γ to give τm.
II.13.3 For Meme 75 we recognize that our four one-manifolds of t, n, m, and p can use the S0 inputs and outputs with values +r and -r to create our plessists and plessemorphs, or biological entities, that enshrine λ through their pointspaces, V0. Those are our nucleotide and DNA grammar. And for Meme 76 we recognize the various pointspaces and their behaviours as contributors to distinct one-manifolds.
II.13.4 Our one-manifolds can now in their turn create their distinct lines and linespaces, S1–V1. There is one for every dimension. This gives values at each point of each of τt, τn, τm, and τp.
II.13.5 However, since these manifolds bound a circulation, then they also state the clock times, T, over which the Ingredients 1, 2, 3 and 4 are each replaced and/or renewed. And since those Ingredients interact with the surroundings, then the one-manifolds are homomorphic. Those absolute times are T for the overall circulation to match τt. The others are TN, TM, and TP with the absolute time intervals matching the various lengths τn, τm, and τp.
Meme 77 then declares that for every point x on each manifold, there exists the neighbourhood N(x) of all points within the distance r, which is a 1-ball stretching between (r - x) and (r + x). And since each point in N(x) contains such a 1-ball whose contents are at least x, then any two neighbourhoods N(x1) and N(x2) have a mapping that finds all points in each, meaning all four manifolds are continuous. And if they are continuous, while their structures are replaced, then these one-manifolds are also homeomorphic.
And for Meme 78, each one-manifold ranges all about its identity, # or S’. Each has a 1-ball that contributes to a projective plane. Each spans a complete circulation. They together form our fibrations and cofibrations, and our biology–replication globe boundaries as they contribute to our mapping cylinder.
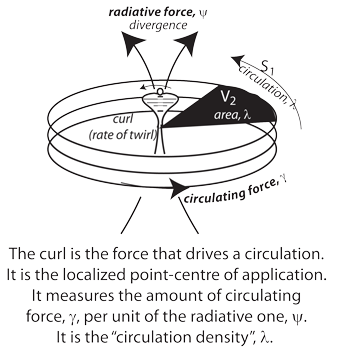
II.13.6 The radiative and circulating forces ψ and γ at work as infinite cyclic subgroups in each of our four one-manifolds produce λ as the infinite cyclic group. They also form the various interconnected S0,1,2,3 biosurfaces that create the self-intersections, the Whitney umbrellas, and the Möbius strips that in their turn bind into the various V1,2,3,4 biovolumes.
The dτ biological force is a circulation along the various manifolds per each unit of radiative force, dψ, exerted per each interval of time, dt. It thereby creates dλ. It is also liable to variation.
Maxwell realized, however, that as in Figure 18, every such circulating flow seeks to close a path at some rate. This is in our case to combine the homomorphic and the homeomorphic, in our manifolds, to create the λ biology as the wind wall.
In a process very similar to the construction of a wind wall, when a pie or cake is being baked, it develops a surrounding crust. We can then slice the result. Since every piece of pie is bounded by a length of crust, there is a definite ratio—a flow rate or curl—between the length of crust, S1, and the piece’s area, V2. Every region is therefore associated with a specific amount of wind wall boundary flow, S1⁄V2. This is the “circulation density” or circulation per unit area. This curl states the volume density force driving the circulation per each interval, but always as a localized point-centre of application. There is a definite wind wall pressure and force per each unit contained. Its rate is dt = Tdτ over the entire circulation.
The curl states the interaction between the biovolume interior, V2, and its surroundings, S1, that lifts towards the mapping cylinder as θ and ρ.
II.13.7 Meme 79 now declares that every pointspace, V0, upon every manifold is also the S0 that drives:
• the fibration and cofibration;
• the pinch point self-intersection;
• the movement about the helicoid;
• the recurvature about a rotahedron; and
• the journey across a projective plane.
II.13.8 Our model now has the archetypal plessemorphs, plesseomes, and plessetopes it needs to describe its population of plessists, plessiomes, and plemes that jointly create both the set of activities as the biological λ, and the surrounding ecology of Mλ. The different recurvatures, wind walls, and interfaces are various combinations of the absolute time spans T, TN, TM, and TP, and the topological manifolds τt, τn, τm, and τp.
II.13.9 And now that we have all the tools we need to examine the structures that transform within our spaces, we must examine the spaces that support those transformations. We can then relate our model to real world biology and ecology as λ.